Mùa hè mang lại cũng là lúc các bạn học sinh lớp 9 đang bận rộn ôn tập để sẵn sàng cho kì thi tuyển sinh vào lớp 10. Vào đó, Toán học là một trong môn thi đề xuất và điểm số của nó luôn luôn được nhân thông số hai. Vậy buộc phải ôn tập môn Toán thế nào thật kết quả đang là thắc mắc của tương đối nhiều em học tập sinh. Phát âm được điều đó, loài kiến guru xin được giới thiệu tài liệu tổng hợp những dạng toán thi vào lớp 10. Trong bài viết này, công ty chúng tôi sẽ lựa chọn lọc các dạng toán cơ bạn dạng nhất trong chương trình lớp 9 cùng thường xuyên lộ diện trong đề thi vào 10 các năm dại dột đây. Ở mỗi dạng toán, chúng tôi đều trình bày cách thức giải và đưa ra phần lớn ví dụ của thể để những em dễ tiếp thu. Những dạng toán bao gồm cả đại số và hình học, ngoài các dạng toán cơ phiên bản thì sẽ sở hữu được thêm các dạng toán nâng cấp để cân xứng với các bạn học sinh khá, giỏi. Khôn xiết mong, đây đang là một bài viết hữu ích cho chúng ta học sinh từ bỏ ôn luyện môn Toán thật tác dụng trong thời hạn nước rút này.
Bạn đang xem: Đề ôn thi cấp 3 toán

Dạng I: Rút gọn gàng biểu thức tất cả chứa căn thức bậc hai
Trong các dạng toán thi vào lớp 10, đấy là dạng toán ta đã học sống đầu chương trình lớp 9.Yêu cầu những em cần phải nắm vững có mang căn bậc nhị số học tập và những quy tắc chuyển đổi căn bậc hai. Shop chúng tôi sẽ chia nhỏ ra làm 2 các loại : biểu thức số học và biểu thức đại số.

1/ Biểu thức số học
Phương pháp:
Dùng các công thức biến đổi căn thức : giới thiệu ; đưa vào ;khử; trục; cộng, trừ căn thức đồng dạng; rút gọn phân số…) nhằm rút gọn biểu thức.
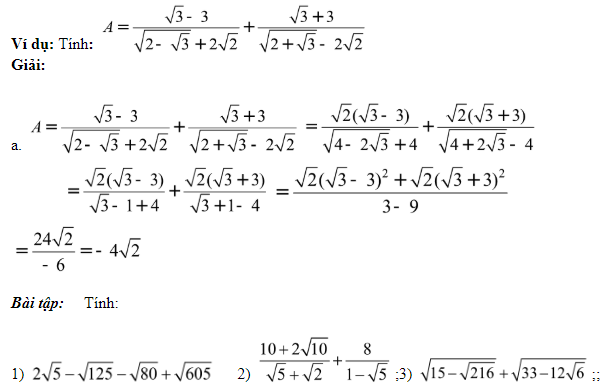
2/ Biểu thức đại số:
Phương pháp:
- Phân tích đa thức tử và mẫu mã thành nhân tử;- tìm kiếm ĐK xác định- Rút gọn gàng từng phân thức- thực hiện các phép thay đổi đồng tuyệt nhất như:+ Quy đồng(đối với phép cùng trừ) ; nhân ,chia.
+ vứt ngoặc: bằng cách nhân 1-1 ; nhiều thức hoặc dùng hằng đẳng thức
+ Thu gọn: cộng, trừ các hạng tử đồng dạng.
+ đối chiếu thành nhân tử – rút gọn
Ví dụ: mang lại biểu thức:
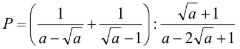
a/ Rút gọn gàng P.
b/ kiếm tìm a để biểu thức p nhận quý giá nguyên.
Giải: a/ Rút gọn P:

Bài tập:
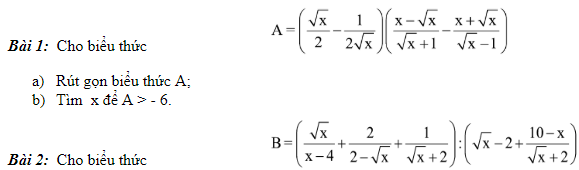
1. Rút gọn gàng biểu thức B;
2. Tìm kiếm x để A > 0
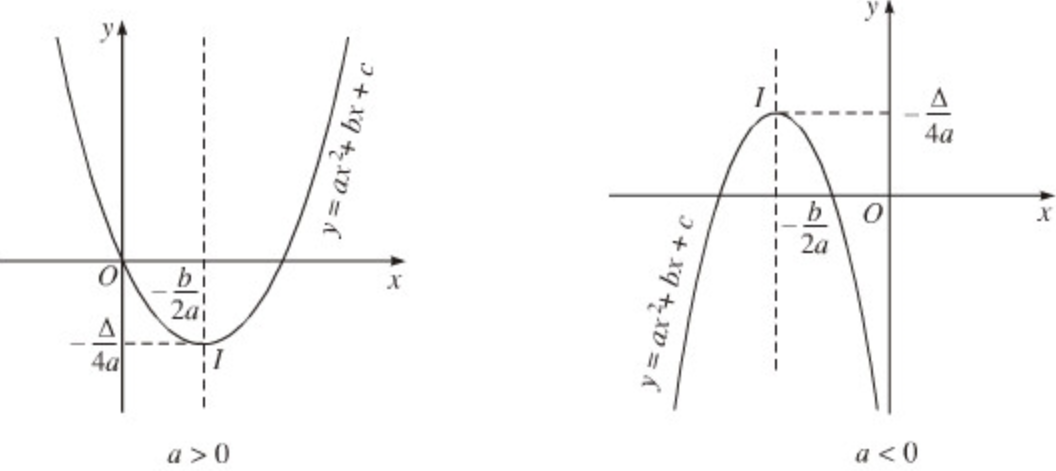
Dạng II: Đồ thị y = ax + b (a ≠ 0) và y = ax2 (a ≠ 0) và tương quan giữa chúng
Trong các dạng toán thi vào lớp 10, thì dạng toán liên quan đến vật thị hàm số yêu thương cầu những em học viên phải thay được khái niệm và bề ngoài đồ thị hàm hàng đầu ( đường thẳng) và hàm bậc nhì (parabol).
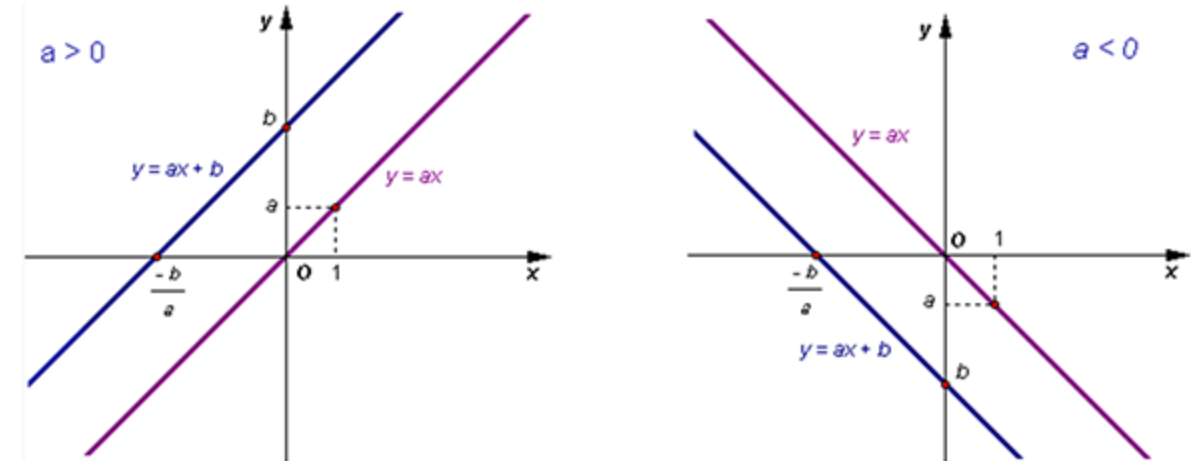
1/ Điểm thuộc đường – đường trải qua điểm.
Phương pháp : Điểm A(x
A; y
A) thuộc đồ thị hàm số y = f(x) y
A = f(x
A).
VD: Tìm thông số a của hàm số: y = ax2 biết đồ thị hàm số của nó trải qua điểm A(2;4)
Giải:
Do đồ vật thị hàm số đi qua điểm A(2;4) nên: 4 = a.22 ⇔ a = 1
2/ giải pháp tìm giao điểm của hai tuyến phố y = f(x) với y = g(x).
Phương pháp:
Bước 1: Hoành độ giao điểm là nghiệm của phương trình f(x) = g(x) (*)
Bước 2: lấy x tìm kiếm được thay vào 1 trong hai cách làm y = f(x) hoặc y = g(x) nhằm tìm tung độ y.
Chú ý: Số nghiệm của phương trình (*) là số giao điểm của hai tuyến đường trên.
3/ quan hệ giữa (d): y = ax + b với (P): y = a’x2 (a’0).
3.1.Tìm tọa độ giao điểm của (d) với (P).Phương pháp:
Bước 1: search hoành độ giao điểm là nghiệm của pt:
a’x2 = ax + b (#) ⇔ a’x2- ax – b = 0
Bước 2: mang nghiệm đó núm vào hàm số y = ax +b hoặc y = ax2 nhằm tìm tung độ y của giao điểm.
Chú ý: Số nghiệm của pt là số giao điểm của (d) cùng (P).
3.2.Tìm đk để (d) và (P) cắt;tiếp xúc; không giảm nhau:Phương pháp:
Từ phương trình (#) ta có: ax2 - ax - b = 0 => Δ = (-a)2 + 4ab
a) (d) cùng (P) giảm nhau ⇔⇔pt bao gồm hai nghiệm sáng tỏ ⇔Δ > 0b) (d) và (P) tiếp xúc với nhau ⇔⇔ pt bao gồm nghiệm kép ⇔ Δ = 0c) (d) và (P) không giao nhau ⇔⇔ pt vô nghiệm ⇔ ΔBài tập về hàm số:
Bài 1. Mang lại parabol (p): y = 2x2.
tìm cực hiếm của a,b làm sao để cho đường trực tiếp y = ax+b xúc tiếp với (p) và trải qua A(0;-2).tìm phương trình con đường thẳng xúc tiếp với (p) tại B(1;2).Tìm giao điểm của (p) với con đường thẳng y = 2m +1.Bài 2: mang đến (P) y = x2 và đường thẳng (d) y = 2x + m
Vẽ (P)Tìm m để (P) tiếp xúc (d)Tìm toạ độ tiếp điểm.Dạng III: Phương trình và Hệ phương trình
Giải phương trình và hệ phương trình là dạng toán cơ phiên bản nhất trong các dạng toán thi vào lớp 10. Giải hệ phương trình sẽ dùng 2 phương thức là rứa và cộng đại số, giải pt bậc hai ta dung cách làm nghiệm. Quanh đó ra, sống đây cửa hàng chúng tôi sẽ ra mắt thêm một số trong những bài toán đựng tham số liên quan đến phương trình

1/ Hệ phương trình bâc tốt nhất một nhì ẩn – giải với biện luận:
Phương pháp:
+ Dạng tổng quát:
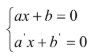
+ biện pháp giải:
Phương pháp thế.Phương pháp cùng đại số.Ví dụ: Giải các HPT sau:

+ thực hiện PP để ẩn phụ. ĐK: x ≠ -1, y≠ 0.

2/ PT bậc nhị + Hệ thức VI-ET
2.1.Cách giải pt bậc hai: ax2 + bx + c = 0 ( a≠ 0)Phương pháp:

Phương pháp:
Nếu x1 , x2 là nghiệm của pt : ax2 + bx + c = 0 (a ≠0) thì
S = x1 + x2 = -b/a p. = x1x2 =c/a.
Đảo lại: Nếu có hai số x1,x2 nhưng mà x1 + x2 = S với x1x2 = p. Thì hai số sẽ là nghiệm (nếu tất cả ) của pt bậc 2: x2 - Sx + phường = 0
3/ Tính giá trị của các biểu thức nghiệm:
Phương pháp: đổi khác biểu thức để làm xuất hiện nay : (x1 + x2) cùng x1x2
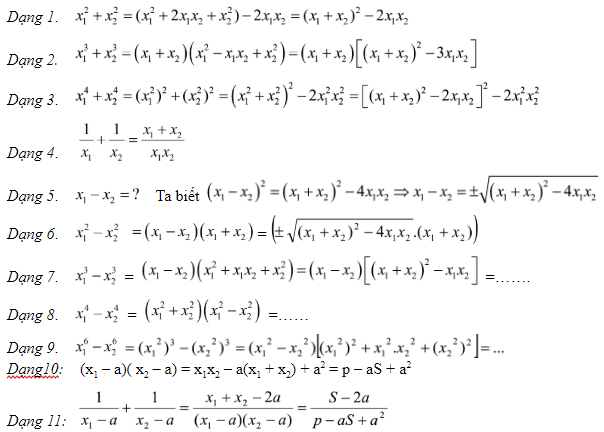
Bài tập :
a) mang lại phương trình : x2 - 8x + 15 = 0. Tính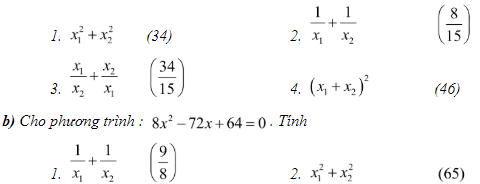
6/ tra cứu hệ thức liên hệ giữa hai nghiệm của phương trình sao cho nó không nhờ vào vào tham số
Phương pháp:
1- Đặt đk để pt kia cho bao gồm hai nghiệm x1 cùng x2
(thường là a ≠ 0 và Δ ≥ 0)
2- Áp dụng hệ thức VI-ET:
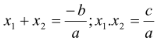
3- phụ thuộc vào hệ thức VI-ET rút tham số theo tổng nghiệm, theo tích nghiệm sau đó đồng hóa các vế.
Ví dụ : mang lại phương trình : (m - 1)x2 - 2mx + m - 4 = 0 (1) tất cả 2 nghiệm x1;x2. Lập hệ thức tương tác giữa x1;x2 làm thế nào cho chúng không phụ thuộc vào m.
Giải:
Theo hệ th ức VI- ET ta cú :
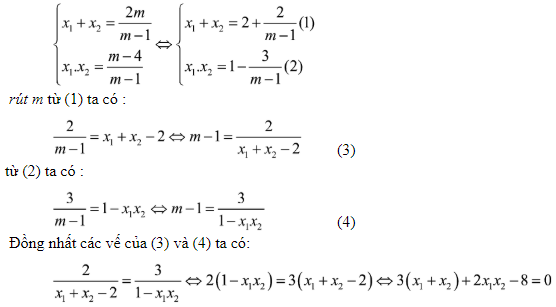
7/ Tìm cực hiếm tham số của phương trình thỏa mãn nhu cầu biểu thức đựng nghiệm vẫn cho:
Phương pháp:
- Đặt đk để pt có hai nghiệm x1 và x2(thường là a ≠ 0 với Δ ≥ 0)
- từ biểu thức nghiệm kia cho, áp dụng hệ thức VI-ET để giải pt.
- Đối chiếu cùng với ĐKXĐ của tham số để xác định giá trị buộc phải tìm.

- chũm (1) vào (2) ta gửi được về phương trình sau: m2 + 127m - 128 = 0 => m1 = 1; m2 = -128
Bài tập
Bài tập 1: cho pt: x2 - 2(m + 3)x + m2 + 3 = 0
a) Giải pt với m = -1 với m = 3b) tìm m để pt bao gồm một nghiệm x = 4c) search m để pt có hai nghiệm phân biệtd) kiếm tìm m để pt gồm hai nghiệm thoả mãn điều kiện x1 = x2Bài tập 2:
Cho pt : ( m + 1) x2 + 4mx + 4m - 1 = 0
a) Giải pt cùng với m = -2b) với mức giá trị nào của m thì pt gồm hai nghiệm phân biệtc) tra cứu m nhằm pt gồm hai nghiệm thoã mãn điều kiện x1 = 2x2
Dạng IV: Giải bài bác toán bằng phương pháp lập phương trình.
Trong các dạng toán thi vào lớp 10, đấy là một dạng toán siêu được quan tiền tâm vừa mới đây vì nó đựng yếu tố ứng dụng thực tế ( vật dụng lí, hóa học, ghê tế, …), đòi hỏi các em phải biết suy luận từ thực tiễn đưa vào phương pháp toán.
Phương pháp:
Bước 1. Lập PT hoặc hệ PT:
-Chọn ẩn, đơn vị cho ẩn, điều kiện tương thích cho ẩn.
-Biểu đạt những đại lượng khác theo ẩn ( chú ý thống nhất 1-1 vị).
-Dựa vào những dữ kiện, đk của câu hỏi để lập pt hoặc hệ pt.
Bước 2 Giải PT hoặc hệ PT.
Bước 3. Xem thêm: Pdf sách toán 12 kết nối tri thức tập 1, sách giáo khoa toán 12 kết nối tri thức tập 1 pdf
Các công thức đề nghị nhớ:

Ví dụ
( Dạng toán đưa động)
Một Ô sơn đi tự A cho B cùng một lúc, Ô tô sản phẩm hai đi tự B về A với tốc độ bằng 2/3 gia tốc Ô tô thứ nhất. Sau 5 giờ chúng gặp nhau. Hỏi từng Ô đánh đi cả quãng đường AB mất bao lâu.
Lời Giải
Gọi thời gian ô sơn đi tự A cho B là x ( h ). ( x>0 );

2. (Dạng toán quá trình chung, công việc riêng )
Một đội thứ kéo dự định mỗi ngày cày 40 ha. Khi thực hiện hằng ngày cày được 52 ha, bởi vậy team không số đông cày chấm dứt trước thời hạn 2 ngày mà hơn nữa cày thêm được 4 ha nữa. Tính diện tích thửa ruộng mà lại đội cần cày theo kế hoạch.
Lời Giải:
Gọi diện tích s mà đội buộc phải cày theo chiến lược là x, ( ha ), ( x> 0).
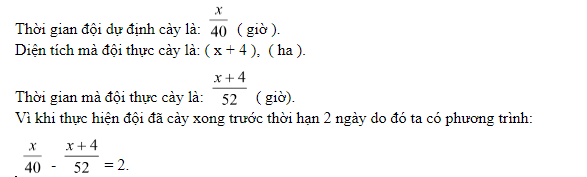
Giải PTBN ta được x= 360. Vậy diện tích mà đội dự tính cày theo kế hoạch là: 360 ha.
Trên phía trên Kiến Guru vừa giới thiệu chấm dứt các dạng toán thi vào lớp 10 hay gặp. Đây là các dạng toán luôn xuất hiện một trong những năm sát đây. Để ôn tập thật xuất sắc các dạng toán này, các em học rất cần phải học thuộc phương pháp giải, xem phương pháp làm từ đầy đủ ví dụ mẫu mã và vận giải quyết những bài tập còn lại. Kỳ thi tuyển sinh vào 10, vẫn vào quá trình nước rút, để đạt được số điểm mình ao ước muốn, tôi mong muốn các em vẫn ôn tập thật cần cù những dạng toán con kiến Guru vừa nêu trên và thường xuyên theo dõi hầu hết tài liệu của con kiến Guru. Chúc những em ôn thi thật tác dụng và đạt tác dụng cao vào kì thi sắp đến tới.
Đề môn Toán thi vào lớp 10 ở thủ đô 3 năm cách đây không lâu về cơ bản không chuyển đổi nhiều mà giữ nguyên cấu trúc, hình thức. Theo dự đoán của các giáo viên, năm nay, nhiều khả năng cấu trúc đề thi vẫn sẽ không thay đổi.
Trong 3 năm ngay gần đây, đề môn Toán thi vào lớp 10 thành phố hà nội đều bao gồm 5 bài toán lớn, mỗi bài bác có các ý nhỏ tuổi được kết cấu theo những mức độ từ nhấn biết, tiếp liền đến vận dụng và vận dụng cao.
Cô Nguyễn Thị Vân, giáo viên Toán của Trường thcs Giảng Võ (quận tía Đình, Hà Nội) mang lại hay, đề thi tuyển chọn sinh vào lớp 10 môn Toán của tp. Hà nội 3 năm gần đây về cơ bạn dạng không chuyển đổi nhiều về bản chất, kết cấu và hình thức.
Theo cô Vân, từ thời điểm năm 2019, đề thi đã khai thác thêm các yếu tố thực tiễn khi chuyển vào bài toán hình học tập không gian. Tuy nhiên mỗi năm, Sở GD-ĐT tp. Hà nội có những kiểm soát và điều chỉnh cho cân xứng với tình hình thực tiễn của năm học cùng kỳ thi, đặc trưng khi mấy năm gần đây chịu ảnh hưởng của dịch bệnh lây lan Covid–19.
Năm 2020, đề thi được điều chỉnh cho cân xứng với yếu tố hoàn cảnh do học viên nghỉ học nhiều ở học kỳ II nên một trong những đơn vị kiến thức và kỹ năng được tập trung kiểm tra ở học kỳ I. Cường độ đề thi nhẹ nhàng hơn so với năm 2019.
Năm 2021, trong toàn cảnh dịch bệnh dịch Covid-19 tình tiết phức tạp ảnh hưởng đến câu hỏi học tập cùng ôn thi của những học sinh, đề thi Toán được reviews là khá nhẹ nhàng, tương xứng với thí sinh. Đặc biệt, thời gian làm bài xích giảm 30 phút, còn 90 phút (thay bởi 120 phút) so với những năm trước.
Đề thi vào lớp 10 môn Toán tại thành phố hà nội năm 2021.Về ma trận, đề thi vẫn tất cả 5 việc lớn, được phân bố ở những kiến thức trong chương trình lớp 9.
Bài 1: Thuộc siêng đề căn bậc hai, căn bậc bố trong lịch trình Toán 9, dạng toán rút gọn gàng biểu thức cất căn cùng các câu hỏi phụ.
Bài 2: bài gồm tất cả 2 câu. Câu 1 thuộc chuyên đề giải bài toán bằng cách lập phương trình hoặc hệ phương trình. Câu 2 thuộc dạng vận dụng hình học tập không gian.
Bài 3: tất cả 2 thắc mắc nhỏ. Câu 1 giải phương trình hoặc hệ phương trình. Câu 2về sự tương giao giữa các đồ thị.
Bài 4: thuộc chủ đề hình học (3 điểm) có 3 câu. Trong đó các câu 1 với câu 2, học tập sinh rất có thể dễ dàng chứng tỏ được. Câu 3 là câu vận dụng cao.
Bài 5: bài nâng cao.
Đề thi có các thắc mắc phân loại học viên ở các câu: câu 3 bài xích 1; ý b) của câu 2 bài 3; câu 3 bài bác 4 (ý 2) và bài bác 5.
“Mặc cho dù về hình thức, thời gian thi rất có thể thay đổi, nhưng kiến thức thi vẫn trung tâm và dính sát cấu tạo đề thi các năm trước. Vì chưng đó, nhằm đạt công dụng làm bài xuất sắc nhất, các học viên nên phân chia thời hạn làm bài hợp lí cho từng câu, làm cho đâu đề nghị cẩn thận, sâu sắc để lấy điểm tối nhiều ở đó.
Các em cần chăm chú các lỗi không đúng rất nhỏ dại trong cách trình bày bài như thiếu điều kiện xác định, không đối chiếu điều kiện, thiếu thốn kết luận, thiếu 1-1 vị, trình bày tắt các bước lập luận… nhằm tránh bị trừ điểm xứng đáng tiếc” - cô Vân chuyển lời khuyên.
Đề thi vào lớp 10 môn Toán tại hà nội thủ đô năm 2020Nói về đề thi 3 năm gần đây, cô giáo Đinh Tuyết Trinh, Trưởng cỗ môn Toán khối thcs của Trường thcs và thpt M.V.Lômônôxốp (quận phái mạnh Từ Liêm, Hà Nội) mang lại hay đề thi vẫn bao hàm 5 việc lớn, mỗi bài xích có những ý nhỏ tuổi được cấu tạo theo các mức độ từ nhận biết, am tường đến vận dụng và vận dụng cao; bảo vệ phân loại học viên và có tính phân một số loại cao.
Chỉ riêng rẽ đề thi của năm học 2021–2022 có sự đổi khác về thời gian làm bài, thay vì 120 phút như những thời gian trước thì chỉ với 90 phút.
“Nội dung, kiến thức của đề thi 3 năm ngay sát đây đảm bảo an toàn tính bất biến và không gây “sốc” cho học sinh khi hiểu đề thi. Tuy vậy, mức độ đề thi vào 10 của năm học 2021–2022 cũng được giảm nhẹ nhàng hơn so với 2 năm trước. Cố gắng thể, sút số ý và sút độ khó cho các câu hỏi, hoàn toàn có thể do thời điểm đó, dịch covid bùng phát, học sinh phải học online đề nghị Sở GD-ĐT điều chỉnh cho phù hợp".
Theo cô Trinh, năm nay cấu trúc đề về cơ phiên bản có lẽ không cố gắng đổi. Học sinh rất có thể bám gần kề vào cấu trúc đề của các năm kia đề làm cho trọng tâm, ôn tập.
“Dù vậy, đề thi luôn luôn có xu hướng thay đổi để thỏa mãn nhu cầu với chương trình nhiều mới. Vì chưng đó, học sinh cũng cần chú ý các vấn đề có liên quan đến thực tiễn - bài xích này khoảng 0,5 điểm” - cô Trinh phân chia sẻ.
Với những nhận định và đánh giá trên, cô Trinh khuyên nhủ các học sinh ôn tập một biện pháp nghiêm túc, nắm chắc kỹ năng và kiến thức cơ bản, ôn tập theo từng công ty đề. Học tập thuộc các công thức, kí hiệu vào từng công thức, né nhầm lẫn những công thức cùng với nhau. Trình bày bài cẩn thận, không quăng quật bước, ko viết tắt kiêng bị mất điểm không xứng đáng có.
Khi làm bài xích cần hiểu kĩ đề, không thải hồi ý, đo lường cẩn thận. Đối với bài xích hình, chăm chú vẽ đúng yêu cầu của đề, hình vẽ đề xuất dễ nhìn, kí hiệu hình mẫu vẽ rõ ràng, vẽ hình bằng bút bi (trừ vẽ đường tròn bởi bút chì). Đặc biệt, cần dành thời hạn để đọc cùng soát lại bài xích làm trước khi nộp bài bác thi.
Đề thi vào lớp 10 môn Toán tại tp hà nội năm 2019Kỳ thi vào lớp 10 công lập của tp hà nội năm ni sẽ ra mắt vào ngày 18-19/6. Các thí sinh dự thi trường siêng sẽ làm bài bác thi môn chuyên vào ngày 20/6.
Năm nay, ngay gần 130.000 sĩ tử của hà nội thủ đô sẽ bước vào mùa thi lớp 10, mặc dù sẽ chỉ có khoảng 69.000 suất vào lớp 10 công lập (không chuyên). Đây là năm bao gồm tỉ lệ chọi vào lớp 10 cao kỉ lục ở hà nội thủ đô trong những năm qua.
Thanh Hùng

Trước kỳ thi vào lớp 10, bài toán thử sức với những đề thi thử giúp học viên làm quen dạng thức đề, rèn tâm lý làm bài, cân đối thời gian cùng thêm sáng sủa khi bước vào thi chủ yếu thức.

Các đề thi môn Ngữ văn vào lớp 10 cùng lớp 10 chuyên của TP.HCM luôn được review cao vị tính thời sự cùng gợi mở.

Đề thi vào lớp 10 môn Toán của tp hcm những năm vừa mới đây thường có 8 câu hỏi với những câu hỏi ứng dụng yên cầu học sinh phải biết vận dụng kiến thức để xử lý.






