bí quyết toán hình 12 có không ít các dạng bài, đôi khi sẽ khiến chúng ta dễ nhầm lẫn. Đừng lo! nội dung bài viết chia sẻ cho cho chúng ta toàn bộ cách làm toán 12 hình học, không chỉ giúp dễ dãi tổng phù hợp kiến thức, ngoài ra mang lại toàn bộ kiến thức toán hình 12 tương đối đầy đủ đến mỗi học tập sinh.
1. Tổng hợp công thức toán hình 12 khối đa diện
Đến cùng với chương thứ nhất - khối nhiều diện, các bạn được học về hình chóp tam giác, chóp tứ giác, hình hộp,... Chúng ta có thể hiểu rằng khối nhiều diện là phần không gian được số lượng giới hạn bởi hình nhiều diện, bao hàm cả hình đa diện đó. Ta sẽ sở hữu những phương pháp như sau:
1.1. Công thức toán hình 12 khối đa diện
Thể tích khối chóp vận dụng cho chóp tam giác và chóp tứ giác:
Công thức tính thể tích hình chóp được hiểu là một trong những phần ba diện tích dưới mặt đáy nhân với chiều cao. Thể tích khối chóp tứ giác phần đa và tam giác đều sở hữu cùng bình thường công thức.
Bạn đang xem: Công thức lớp 12 môn toán
Ta có thể tích khối chóp:

Trong đó:
S đáy:Diện tích mặt đáyh: Độ dài chiều caoThể tích khối chóp S.ABCD là:

1.2. Công thức toán hình 12 khối lăng trụ
Hình lăng trụ bao gồm vài đặc điểm giống nhau, kia là:
Nằm trên 2 khía cạnh phẳng tuy vậy song cùng nhau và tất cả hai lòng giống nhau.
Cạnh bên đôi một bằng nhau và tuy vậy song với nhau, các mặt mặt là hình bình hành.


Thể tích khối lăng trụ được tính bằng cách làm như sau:
V= S.h
Trong đó:
S là diện tích đáy.h là chiều cao.Lưu ý: Hình lăng trụ đứng bao gồm chiều cao đó là cạnh bên.
Ngoài ra, những em tất cả thể đọc thêm công thức tính thể tích khối lăng trụ tam giác đềuđể giải những bài tập về hình lăng trụ.
1.3.Thể tích hình vỏ hộp chữ nhật lớp 12
Hình hộp chữ nhật có những cạnh lòng lần lượt là a, b và chiều cao c, khi ấy thể tích hình vỏ hộp chữ nhật là V= a.b.c (a, b, c gồm cùng đơn vị).
Hình lập phương là dạng đặc biệt của hình hộp chữ nhật tất cả a = b = c. Do thế thể tích hình lập phương được tính theo công thức: V = a3
1.4.Công thức toán hình 12 khối chóp cụt
Hình chóp cụt được tư tưởng là một phần của khối nhiều diện ở giữa mặt đáy và thiết diện cắt do đáy của hình chóp và một khía cạnh phẳng tuy vậy song cùng với đáy.
a) diện tích xung quanh hình chóp cụtDiện tích bao bọc của hình chóp cụt là diện tích các mặt xung quanh, phần bao bọc hình chóp cụt không bao hàm diện tích nhì đáy.
Diện tích hình chóp cụt đều được tính bằng cách làm dưới đây:


Trong đó:
Sxq: diện tích xung quanh.n: số lượng mặt bên.a, b: chiều lâu năm cạnh của 2 đáy trên với dưới của hình chóp cụt.h: chiều cao mặt bên.Công thức tính diện tích s xung xung quanh của hình chóp cụt là tính diện tích từng mặt mặt của hình chóp cụt theo công thức tính diện tích s hình thang bình thường, tiếp nối tính tổng diện tích s của tất cả các hình cấu thành những hình chóp cụt.
Nắm trọn tổng thể công thức và phương pháp giải số đông dạng bài bác tập Toán hình 12 cùng với bộ bí quyết độc quyền của VUIHOC ngay!!!
b) bí quyết tính diện tích toàn phầnDiện tích toàn phần của hình chóp cụt được xem bằng tổng diện tích s 2 dưới đáy và diện tích xung xung quanh của hình chóp cụt đó.
Công thức:
Stp = Sxq + Sđáy phệ + Sđáy nhỏ
Trong đó:
Stp: diện tích s toàn phầnSxq: diện tích s xung quanh
Sđáy lớn: diện tích đáy lớn
Sđáy nhỏ: diện tích đáy nhỏc) Thể tích hình chóp cụt được tính bằng công thức
Công thức:
Trong đó:
V: thể tích hình chóp cụt.
S, S’ theo lần lượt là diện tích dưới đáy lớn và đáy nhỏ dại của hình chóp cụt.
h: chiều cao (khoảng cách giữa 2 dưới đáy lớn với đáy nhỏ)
2. Cách làm toán hình 12 hình nón
Có thể hiểu đơn giản, hình học có không gian ba chiều mà mặt phẳng phẳng và mặt phẳng cong hướng lên phía trên là hình nón. Đầu nhọn của hình nón được gọi là đỉnh và mặt phẳng phẳng được điện thoại tư vấn là đáy. Ta hoàn toàn có thể dễ dàng bắt gặp những đồ vật dụng có hình nón như loại nón lá, mũ sinh nhật,...
a) diện tích s xung quanh hình nón được tính bằng tích của số Pi (π) nhân với nửa đường kính đáy hình nón (r) rồi nhân với con đường sinh hình nón (l). Ta có công thức:

Trong đó:
Sxq: là diện tích s xung quanh.π: là hằng sốr: là cung cấp kính mặt đáy hình nónl: con đường sinh của hình nón.b) diện tích s toàn phần hình nón được tính bằng diện tích xung quanh hình nón cộng với diện tích mặt đáy của hình nón.

Vì diện tích của dưới đáy là hình trụ nên ta vận dụng công thức tính diện tích s hình tròn:

c) Để tính thể tích khốinón, ta áp dụng công thức sau:

Trong đó:
V: ký kết hiệu thể tích hình nónπ: = 3,14r: buôn bán kính hình tròn đáy.h: là con đường cao tính từ đỉnh hình nón xuống trọng điểm đường trònd) Tổng hợp một vài phương pháp mặt nón:
Đường cao: h=SO (hay còn được gọi là trục của hình nón)
Bán kính đáy: r=OA=OB=OM
Đường sinh: l=SA=SB=SM
Góc sinh hoạt đỉnh: ASB
Thiết diện qua trục SAB cân tại S
Góc giữa dưới đáy và con đường sinh: SAO=SBO=SMO
Chu vi đáy:

Diện tích đáy: Sđáy

PAS VUIHOC – GIẢI PHÁP ÔN LUYỆN CÁ NHÂN HÓA
Khóa học tập online ĐẦU TIÊN VÀ DUY NHẤT:
⭐Xây dựng lộ trình học từ mất gốc mang đến 27+
⭐Chọn thầy cô, lớp, môn học theo sở thích
⭐Tương tác trực tiếp nhì chiều thuộc thầy cô
⭐ Học đi học lại đến khi nào hiểu bài bác thì thôi
⭐Rèn tips tricks góp tăng tốc thời hạn làm đề
⭐ khuyến mãi full bộ tài liệu độc quyền trong quy trình học tập
Đăng cam kết học demo miễn phí ngay!!
3. Phương pháp toán hình lớp 12 hình trụ
Hình được số lượng giới hạn bởi hai đường tròn xuất hiện trụ và đường kính bằng nhau được hotline là hình trụ. Trong cách làm toán hình lớp 12, hình trụ cũng khá được tìm kiếm tương đối nhiều, áp dụng cho tất cả dạng bài phức hợp và solo giản.
a) cách làm tính thể tích khối trụ:

Trong kia ta có:
r: nửa đường kính hình trụh: độ cao hình trụ
b) diện tích s xung xung quanh của khối trụ có công thức như sau:

Trong đó:
r: nửa đường kính hình trụh: độ cao nối trường đoản cú đáy tính đến đỉnh của hình trục) công thức tính diện tích toàn phần


d) Một vài phương pháp hình trụ khác
Diện tích đáy:

Chu vi đáy:

4. Những phương pháp toán hình lớp 12: khía cạnh cầu
Theo đông đảo gì họ đã được học, mặt cầu tâm O, bán kính r được khiến cho bởi tập đúng theo điểm M trong không gian và biện pháp điểm O khoảng cố định không đổi bởi r (r>0).
Cho mặt ước S (I,R), ta có:
Trong đó: r: bán kính hình cầu
Diện tích khía cạnh cầu:

5. Phương pháp toán hình 12 tọa độ trong ko gian
5.1. Hệ tọa độ oxyz
Trong không gian với hệ tọađộ oxyz, cho ba trục Ox, Oy, Oz vuông góc từng song một và rõ ràng nhau, có gốc tọa độ O, trục tung Oy, trục hoành Ox, trục cao Oz và những mặt tọa độ Oxy, Oyz, Ozx. Các


Chú ý:


5.2. Vectơ

5.3. Tích có hướng của 2 vectơ
Cho 2 vectơ







Tính hóa học có hướng của 2 vectơ
a.



b.

c.


5.4. Tọa độ điểm

5.5. Phương trình phương diện cầu, đường thẳng, khía cạnh phẳng
a) Phương trình đường thẳng
Các dạng phương trình con đường thẳng trong không gian bao gồm:
- Vectơ chỉ phương của đường thẳng:
Định nghĩa: mang đến đường thẳng d. Ví như vectơ


Chú ý:
a là VTCP của d thì
Nếu d đi qua hai điểm A, B thì AB là 1 trong VTCP của d
Trục Ox tất cả vecto chỉ phương






- Phương trình thông số của con đường thẳng:
Phương trình thông số của con đường thẳng () đi qua điểm


{x=x0+a1t
{y=y0+a2t
z= z0+a3t
- Phương trình chủ yếu tắc của đường thẳng:
Phương trình thiết yếu tắc của đường thẳng (



(


b) Phương trình khía cạnh cầu
Theo định nghĩa, chúng ta có thể biết được, phương trình mặt cầu là lúc cho điểm I thắt chặt và cố định và số thực dương R. Gọi tập hợp đa số điểm M trong không gian cách I một khoảng R được hotline là mặt mong tâm I, nửa đường kính R.
Lúc này ta gồm hai dạng phương trình:
Dạng 1: Phương trình mặt mong (S), bao gồm tâm I (a,b,c), bán kính R

Dạng 2: Phương trình tất cả dạng:

Với điều kiện là:


c) Phương trình khía cạnh phẳng
- Phương trình phương diện phẳng a:
Phương trình tổng quát:


Phương trình đoạn chắn:

( a qua A (a;0;0) ; B ( 0;b;0 ) ; C (0;0;c ))
- Góc giữa 2 mặt phẳng:
a: Ax + By + Cz + D = 0
b: A’x +B’y + C’z + D’ = 0

- khoảng cách từ điểm M0(x0; y0; z0) mang lại mặt phẳng a:
$d(M,(a))=fracAx_0+By_0+Cz_0+DsqrtA^2+B^x+C^2^$
Đăng cam kết ngay để được những thầy cô tổng hợp kỹ năng toán 12 và xây dừng lộ trình ôn thi THPT non sông sớm ngay từ bây giờ
Hy vọngcác công thức toán hình 12mà VUIHOC chia sẻ trên trên đây phần làm sao giúp chúng ta ghi nhớ kết quả và và tinh giảm sai sót trong quá trình làm bài. Nếu ước muốn hiểu sâu về bài bác giảng kỹ năng và kiến thức Toán 12, chúng ta học sinh hãy đăng ký tham gia khóa học giành cho học sinh lớp 12 ôn thi Toán trung học phổ thông Quốc Gia trên Vuihoc.vn nhé! Chúc các bạn ôn thi thật hiệu quả.
Nội dung thi THPT giang sơn 2020 môn Toán trải rộng từ lớp 11 cho tới lớp 12, trong đó kiến thức triệu tập chủ yếu đuối là chương trình lớp 12. Bởi vậy, cỗ công thức giải cấp tốc toán 12 là một trong những điều đặc biệt quan trọng mà các bạn phải trang bị cho phiên bản thân mình. Hiểu được điều đó, trong bài viết này, kiến guru xin chia sẻ đến chúng ta một số công thức giải nhanh toán 12 phổ cập nhất. Hi vọng qua bài xích viết, các các bạn sẽ củng chũm thêm kiến thức và kỹ năng cho chính mình, chuẩn bị thật tốt để bước vào kì thi trung học phổ thông Quốc gia.

I. Một trong những công thức giải cấp tốc toán 12 phần đại số.
Xem thêm: Toán 10 5.8 - toán học lớp 10
1. Những công thức giải cấp tốc toán 12 logarit
Điều quan trọng đặc biệt để giải cấp tốc là họ cần nắm rõ các phương pháp toán học tập lớp 12 một cách thuần thục. Tiếp sau đây sẽ là cách làm về logarit và bài bác tập.
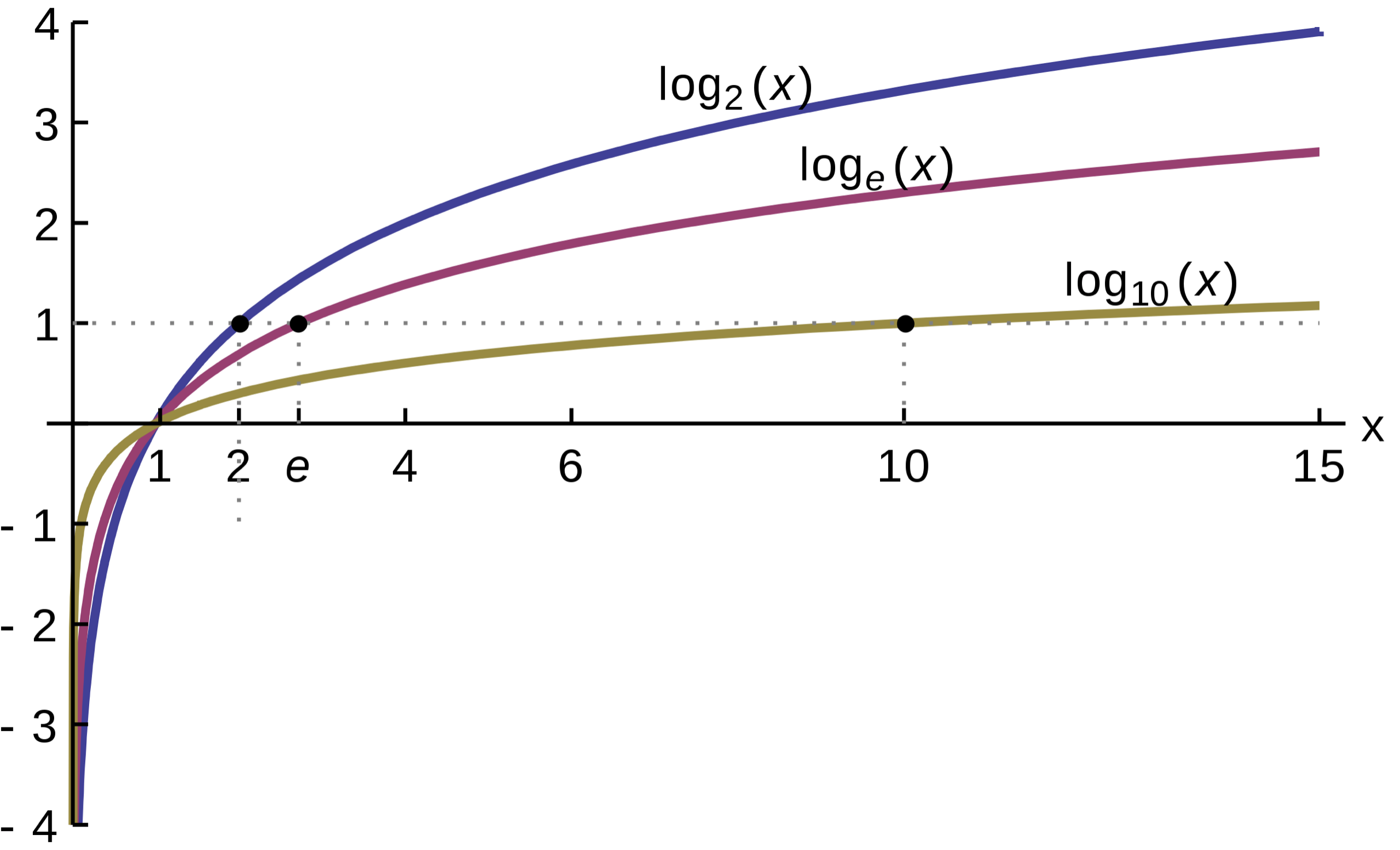
Các công thức Logarit tiếp sau đây chỉ có ý nghĩa khi đối số với cơ số của logarit là dương, đk cơ số a # 1 hoặc 0.
a. Log1a= 0 lúc đối số bởi 1 thì hiệu quả trả ra của logarit bởi 0.
⇒ bài bác tập: log13=0
b. Log1/xa=-logx3 tức thị 1/x=x-1
⇒ bài xích tập: log21/3=-log32c.

Biến đổi cơ số là tên gọi của công thức. Tác dụng trả ra trường đoản cú logarit mới tất cả đối số a của mẫu số biến hóa thành cơ số new và đối số x của tử số thành đối số mới.⇒ bài xích tập: log52=(log5/log2)
d. Logaa=1
⇒ bài bác tập:log22=1
e. Logaxy=logxa+logya
Logarit của một tổng được đưa thành tổng hai logarit
⇒ bài tập: log162=log82+log22=log42+log22+1=log22+log22+1+1=4

g. Logx/ya=log-xalogya
Logarit của phép phân tách được chuyển thành hiệu của 2 logarit.
⇒ bài bác tập: log25/3=log52-log32
Áp dụng những công thức giải nhanh toán 12 trên vào những bài tập sauBài tập 1. Chọn lời giải đúng trong phát biểu về hàm số y=lnx/x
A. Hàm số trên không có cực trị.B. Hàm số trên chỉ gồm một điểm rất đại.C. Hàm số trên chỉ tất cả một điểm cực tiểu.
D. Hàm số có một điểm rất tiểu cùng một điểm rất đại.
Hướng dẫn
Chọn đáp án CTập xác định

Hàmy"đổi dấu từ âm lịch sự dương khi quax=enênx=elà điểm cực tiểu của hàm số.
Bài tập 2.Mệnh đề làm sao sau đó là mệnh đề đúng?
A. Nằm bên cạnh phải trục tung là đồ dùng thị hàm số lôgarit.B. Nằm sát trái trục tung là thiết bị thị hàm số lôgarit.C. Nằm bên cạnh phải trục tung là vật thị hàm số mũ.D. Đồ thị của hàm số mũ nằm phía trái của trục tung.
Hướng dẫn
Chọn đáp án A
Khi x>0 Hàm số lôgarit khẳng định nên đồ gia dụng thị hàm số nằm cạnh sát phải trục tung.
Bài tập 3.Chọn lời giải nào sai trong các phát biểu sau?
A. Vị trí kha khá của thứ thị hàm số mũ với số nón âm luôn luôn có nhì tiệm cận.B. Vị trí kha khá của đồ vật thị hàm số mũ không nằm bên dưới trục hoành.C. Vị trí tương đối của đồ dùng thị hàm số lôgarit nằm bên phải trục tung.
D. Vị trí kha khá của thứ thị hàm số logarit là trên trục hoành.
Hướng dẫn
Chọn đáp án DĐồ thị hàm số logarit nằm cạnh sát phải trục tung cùng cả dưới, cả bên trên trục hoành.
Bài tập 4. Biết logba=2, logca=-3. Vậy công dụng trả ra của biểu thức

Hướng dẫn
Ta tất cả

Chọn A là đáp án

2. Tổng hợp phương pháp giải nhanh toán trắc nghiệm 12 thiết bị thị

II. Một trong những công thức giải nhanh toán lớp 12 phần hình học.
1. Các công thức toán học tập lớp 12 của khối nhiều diện.


- toàn bộ các khía cạnh sẽ là 1 trong những tam giác đều
- Một đỉnh bất kì sẽ có được đỉnh phổ biến với đúng 4 mặt
- gồm số đỉnh (Đ); số mặt (M); số cạnh (C) theo lần lượt là D=6, M=8, C=12. D=6, M=8, C=12.
- các mặt của khối chén bát diện mọi cạnh ađều bao gồm diện là

- gồm 9 khía cạnh phẳng đối xứng
- Khối chén diện những cạnh a sẽ có thể tích là
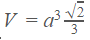
- Mặt mong ngoại tiếp sẽ sở hữu bán kính

Tất cả các mặt sẽ là 1 trong những hình vuông
- Một đỉnh bất kì sẽ sở hữu đỉnh thông thường với đúng 3 mặt
- Số khía cạnh (M); Số đỉnh (Đ); Số cạnh (C) thứu tự là D=8, M=6, C=12, D=8, M=6, C=12.
- tất cả các phương diện khối lập phương có diện tích s là S=6a2.
- Có tất cả 9 phương diện phẳng đối xứng
- Khối lập phương cạnh a sẽ có diện tích là V=a3.
- Mặt ước ngoại tiếp có nửa đường kính

- toàn bộ các phương diện sẽ là một trong ngũ giác đều
- Một đỉnh bất kì sẽ sở hữu đỉnh bình thường với đúng bố mặt
- Số khía cạnh (M); Số đỉnh (Đ); Số canh (C) theo thứ tự là D=20 , M=12 C=30.D=20, M=12, C=30.
- các mặt của khối 12 mặt đều có diện là

- Có tất cả 15 khía cạnh phẳng đối xứng
- Thể tích khối 12 mặt phần đa cạnh a là

- Mặt cầu ngoại tiếp có bán kính là

2. Tổng hợp công thức giải nhanh toán trắc nghiệm 12 thường chạm mặt khác.


Hi vọng với các công thức giải nhanh toán 12 đã giúp chúng ta đọc dành được kiến thức quan trọng cho kì thi chuẩn bị tới. Hình như Đừng ngần ngại hỏi anh em hoặc thầy cô khi bạn chạm chán phải những câu ko hiểu. Hãy tham khảo thêm các bài viết của Kiến để củng nuốm thêm kiến thức bạn nhé.









