Doc.com KHÔNG quảng cáo, cùng tải file cực nhanh không ngóng đợi.
Bạn đang xem: Tổng hợp các dạng toán nâng cao lớp 5

Một số chia hết cho 3 lúc tổng những chữ số của số đó phân tách hết cho 3. Tổng các chữ số của A là 1995 x 7. Do 1995 phân tách hết mang đến 3 nên 1995 x 7 phân tách hết mang lại 3.

1995 chữ số 7
Một số hoặc phân chia hết mang lại 3 hoặc phân tách cho 3 mang đến số dư là 1 hoặc 2.
Chữ số tận cùng của A là 7 không chia hết cho 3, cơ mà A phân tách hết đến 3 cần trong phép phân chia của A mang lại 3 thì số ở đầu cuối chia đến 3 cần là 27. Vậy chữ số tận thuộc của thương vào phép chia A đến 3 là 9, mà lại 9 x 2 = 18, cho nên vì vậy số A/3 x 0,2 là số bao gồm phần thập phân là 8.
Vì vậy khi phân tách A = 777...77777 đến 15 sẽ tiến hành thương bao gồm phần thập phân là 8.
1995 chữ số 7
Nhận xét: Điều chủ quản trong giải mã bài toán bên trên là việc biến đổi A/15 = A/3 x 0,2. Tiếp đến là chứng tỏ A phân chia hết mang lại 3 với tìm chữ số tận thuộc của thương trong phép phân tách A đến 3. Ta rất có thể mở rộng bài toán trên tới câu hỏi sau:
Bài 2 (1*): tra cứu phần thập phân của thương trong phép phân chia số A mang đến 15 biết rằng số A bao gồm n chữ số a với A chia hết mang đến 3?
Nếu kí hiệu A = aaa...aaaa cùng giả thiết A phân tách hết cho 3 (tức là n x a phân chia hết đến 3), thì lúc đó giống như như bí quyết giải việc n chữ số a
1 ta tìm được phần thập phân của yêu mến khi phân tách A mang đến 15 như sau:
- với a = 1 thì phần thập phân là 4 (A = 111...1111, cùng với n chia hết mang đến 3)n chữ số 1
- với a = 2 thì phần thập phân là 8 (A = 222...2222, cùng với n phân chia hết mang đến 3).n chữ số 2
- với a = 3 thì phần thập phân là 2 (A = 333...3333 , cùng với n tùy ý).n chữ số 3
- cùng với a = 4 thì phần thập phân là 6 (A = 444...4444 , cùng với n phân chia hết cho 3)n chữ số 4
- với a = 5 thì phần thập phân là 0 (A = 555...5555, cùng với n phân tách hết mang lại 3).n chữ số 5
- cùng với a = 6 thì phần thập phân là 4 (A = 666...6666, cùng với n tùy ý)n chữ số 6
- với a = 7 thì phần thập phân là 8 (A = 777...7777, cùng với n phân tách hết đến 3)n chữ số 7
- cùng với a = 8 thì phần thập phân là 2 (A = 888...8888, với n chia hết đến 3)n chữ số 8
- với a = 9 thì phần thập phân là 6 (A = 999...9999, với n tùy ý).n chữ số 9
Trong những bài toán 1 với 2 (1*) sinh sống trên thì số chia phần đa là 15. Hiện nay ta xét tiếp một ví dụ mà lại số chia không phải là 15.
Bài 4: Cho mảnh bìa hình vuông ABCD. Hãy cắt từ mảnh bìa kia một hình vuông vắn sao cho diện tích s còn lại bằng diện tích của miếng bìa đã cho.
Bài giải:
Theo đầu bài bác thì hình vuông ABCD được ghép bởi vì 2 hình vuông nhỏ và 4 tam giác (trong đó có 2 tam giác to, 2 tam giác con). Ta thấy rất có thể ghép 4 tam giác bé để được tam giác to mặt khác cũng ghép 4 tam giác bé để được 1 hình vuông vắn nhỏ. Vậy diện tích của hình vuông vắn ABCD chính là diện tích của 2 + 2 x 4 + 2 x 4 = 18 (tam giác con).
Do đó diện tích s của hình vuông vắn ABCD là:

Bài 5: Tuổi ông rộng tuổi con cháu là 66 năm. Biết rằng tuổi ông bao nhiêu năm thì tuổi cháu bấy nhiêu tháng. Hãy tính tuổi ông với tuổi con cháu (tương tự bài Tính tuổi - hội thi Giải toán qua thư TTT số 1).
Giải
Giả sử cháu 1 tuổi (tức là 12 tháng) thì ông 12 tuổi.
Lúc đó ông hơn cháu: 12 - 1 = 11 (tuổi)
Nhưng thực tế ông hơn con cháu 66 tuổi, tức là gấp 6 lần 11 tuổi (66 : 11 = 6).
Do đó thực chất tuổi ông là: 12 x 6 = 72 (tuổi)
Còn tuổi cháu là: 1 x 6 = 6 (tuổi)
Thử lại 6 tuổi = 72 tháng; 72 - 6 = 66 (tuổi)
Đáp số: Ông: 72 tuổi
Cháu: 6 tuổi
Bài 6: Một vị phụ huynh học viên hỏi thầy giáo: "Thưa thầy, vào lớp có bao nhiêu học sinh?" Thầy cười và trả lời: "Nếu gồm thêm một số trong những trẻ em bằng số hiện bao gồm và thêm một phần hai số đó, rồi lại thêm 1/4 số đó, rồi cả thêm con của quý vị (một lần nữa) thì đã vừa tròn 100". Hỏi lớp bao gồm bao nhiêu học sinh?
Giải:
Theo đầu bài xích thì tổng của tất cả số HS và toàn bộ số HS và 50% số HS với 1/4 số HS của lớp vẫn bằng: 100 - 1 = 99 (em)
Để tìm được số HS của lớp ta rất có thể tìm trước 1/4 số HS cả lớp.
Giả sử 1/4 số HS của lớp là 1 trong những em thì cả lớp có 4 HS
Vậy: 50% số HS của lớp là: 4 : 2 = 2 (em).
Suy ra tổng nói bên trên bằng: 4 + 4 + 2 + 1 = 11 (em)
Nhưng thực tế thì tổng ấy phải bởi 99 em, vội 9 lần 11 em (99 : 11 = 9)
Suy ra số HS của lớp là: 4 x 9 = 36 (em)
Thử lại: 36 + 36 + 36/2 + 36/4 + 1 = 100
Đáp số: 36 học sinh.
Bài 7: thâm nhập hội khoẻ Phù Đổng huyện có tất cả 222 ước thủ thi đấu hai môn: bóng đá và bóng chuyền. Mỗi nhóm bóng đá có 11 người. Mỗi nhóm bóng chuyền có 6 người. Biết rằng gồm cả thảy 27 đội bóng, hãy tính số đội bóng đá, số đội bóng chuyền.
Giải
Giả sử có 7 đội bóng đá, thế thì số team bóng chuyền là:
27 - 7 = 20 (đội nhẵn chuyền)
Lúc đó tổng số ước thủ là: 7 x 11 + 20 x 6 = 197 (người)
Vậy ý muốn cho toàn bô người tăng lên 25 thì số dội bống chuyền yêu cầu thay bằng đội bóng đá là:
25 : 5 = 5 (đội)
Do đó, số team bóng chuyền là: đôi mươi - 5 = 15 (đội)
Còn số đội soccer là: 7 + 5 = 12 (đội)
Đáp số: 12 đội bóng đá, 15 team bóng chuyền.
Bài 8: Số gà nhiều hơn số thỏ là 28 con. Số chân gà nhiều hơn thế nữa số chân thỏ là 40 chân. Hỏi có bao nhiêu con gà, bao nhiêu con thỏ?
Giải
Giả sử có 10 nhỏ thỏ, cố thì có: 10 + 28 = 38 (con)
Số chân con kê là: 38 x 2 = 76 (chân)
Số chân thỏ là: 10 x 4 = 40 (chân)
Hiệu số chân gà và thỏ là: 76 - 40 = 36 (chân)
Vì thực tế thì số chân gà hơn số chân thỏ tới 40 chân cần ta bắt buộc tìm phương pháp thêm vào hiệu trên: 40 - 36 = 4 (chân)
Để hiệu số chân tạo thêm 4 thì số thỏ với gà bắt buộc bớt đi là : 4 : 2 = 2 (con)
Vậy số thỏ là: 10 - 2 = 8 (con thỏ)
Số con gà là: 38 - 2 = 36 (con gà)
Đáp số là : 36 nhỏ gà và 8 con thỏ
Bài 9: Một ô tô đi trường đoản cú A cho B với gia tốc 30 km/giờ. Tiếp đến đi từ B về A với vận tốc 45 km/giờ. Tính quãng mặt đường AB biết thời hạn đi trường đoản cú B về A không nhiều hơn thời hạn đi từ bỏ A mang đến B là 40 phút.
Giải:
Tỉ số giữa tốc độ đi và gia tốc về trên quãng đường AB là: 30 : 45 = 2/3.
Vì quãng đường đồng nhất nên gia tốc và thời hạn là hai đại lượng tỉ lệ thành phần nghịch với nhau. Cho nên vì vậy tỉ số thời hạn đi và thời hạn về là 3/2.
luận, ta trả sử số tự nhiên cần tìm kiếm được chia ra thành 51 phần bởi nhau. Lúc ấy 1/3 số đó là 51 : 3 = 17 (phần) ; 1/17 số chính là 51 : 17 = 3 (phần).
Vì 17 : 3 = 5 (dư 2) đề nghị 2 phần của số đó có giá trị là 100 suy ra số chính là :
100 : 2 x 51 = 2550.
Bài 10: Tích tiếp sau đây có tận cùng bằng văn bản số nào?
Bài giải
Tích của bốn thừa số 2 là 2 x 2 x 2 x 2 = 16 với 2003 : 4 = 500 (dư 3) phải ta hoàn toàn có thể viết tích của 2003 quá số 2 dưới dạng tích của 500 team (mỗi nhóm là tích của tứ thừa số 2) với tích của bố thừa số 2 còn lại.
Vì tích của những thừa số có tận cùng là 6 cũng là số bao gồm tận cùng bởi 6 đề nghị tích của 500 team trên gồm tận thuộc là 6.
Do 2 x 2 x 2 = 8 nên khi nhân số có tận cùng bằng 6 với 8 thì ta được số bao gồm tận cùng bằng 8 (vì 6 x 8 = 48). Vậy tích của 2003 thừa số 2 sẽ là số có tận cùng bởi 8.
Bài 11: Một tín đồ mang cam đi thay đổi lấy táo apple và lê. Cứ 9 trái cam thì đổi được 2 quả táo bị cắn dở và 1 trái lê, 5 quả táo khuyết thì đổi được 2 quả lê. Nếu tín đồ đó đổi hết số cam mang đi thì được 17 quả hãng apple và 13 trái lê. Hỏi bạn đó đưa theo bao nhiêu trái cam?
Bài giải
9 trái cam đổi được 2 quả apple và 1 trái lê phải 18 quả cam đổi được 4 quả táo bị cắn dở và 2 quả lê. Vì chưng 5 quả táo đổi được 2 quả lê yêu cầu 18 trái cam đổi được: 4 + 5 = 9 (quả táo).
Do kia 2 trái cam đổi được 1 quả táo. Cứ 5 quả táo khuyết đổi được 2 quả lê yêu cầu 10 trái cam thay đổi được 2 trái lê. Vậy 5 quả cam đổi được một quả lê. Số cam fan đó đưa theo để thay đổi được 17 quả táo và 13 trái lê là : 2 x 17 + 5 x 13 = 99 (quả).
Bài 12: Tìm một số trong những tự nhiên làm sao để cho khi mang 1/3 số đó phân chia cho 1/17 số kia thì có dư là 100.
Bài giải
Vì 17 x 3 = 51 đề xuất để dễ dàng lí luận, ta trả sử số tự nhiên và thoải mái cần kiếm được chia ra thành 51 phần bằng nhau. Lúc đó 1/3 số chính là 51 : 3 = 17 (phần) ; 1/17 số sẽ là 51 : 17 = 3 (phần).
Vì 17 : 3 = 5 (dư 2) bắt buộc 2 phần của số đó có mức giá trị là 100 suy ra số chính là :
100 : 2 x 51 = 2550.
Bài 13: Tuổi của con hiện nay bằng 1/2 hiệu tuổi của cha và tuổi con. Bốn năm trước, tuổi con bởi 1/3 hiệu tuổi của ba và tuổi con. Hỏi khi tuổi con bởi 1/4 hiệu tuổi của cha và tuổi của con thì tuổi của mỗi cá nhân là bao nhiêu?
Bài giải
Hiệu số tuổi của bố và nhỏ không đổi. Trước đây 4 năm tuổi con bởi 1/3 hiệu này, cho nên 4 năm chính là : 1/2 - 1/3 = 1/6 (hiệu số tuổi của cha và con).
Số tuổi ba hơn bé là : 4 : 1/6 = 24 (tuổi).
Khi tuổi con bằng 1/4 hiệu số tuổi của ba và nhỏ thì tuổi con là:
24 x 1/4 = 6 (tuổi).
Lúc đó tuổi bố là : 6 + 24 = 30 (tuổi).
Bài 14: Hoa có một sợi dây dài 16 mét. Bây chừ Hoa đề nghị cắt đoạn dây đó để có đoạn dây tương đối dài 10 mét mà trong tay Hoa chỉ có một chiếc kéo. Các bạn có biết Hoa cắt chũm nào không?
Bài giải
Cách 1: Gập song sợi dây tiếp tục 3 lần, lúc đó sợi dây vẫn được chia thành 8 phần bởi nhau.
Độ dài mỗi phần phân tách là : 16 : 8 = 2 (m)
Cắt đi 3 phần đều nhau thì còn lại 5 phần.
Khi đó độ lâu năm đoạn dây còn sót lại là : 2 x 5 = 10 (m)
Cách 2: Gập đôi sợi dây liên tục 2 lần, lúc ấy sợi dây đã được phân thành 4 phần bằng nhau.
Độ lâu năm mỗi phần phân tách là : 16 : 4 = 4 (m)
Đánh dấu một trong những phần chia tại 1 đầu dây, phần đoạn dây còn lại được gập đôi lại, cắt đi một phần ở đầu bên đó thì độ lâu năm đoạn dây giảm đi là : (16 - 4) : 2 = 6 (m)
Do đó độ dài đoạn dây sót lại là : 16 - 6 = 10 (m)
Bài 15: Một thửa ruộng hình chữ nhật được chia thành 2 mảnh, một mảnh nhỏ trồng rau cùng mảnh sót lại trồng ngô (hình vẽ). Diện tích của mảnh trồng ngô cấp 6 lần diện tích s của mảnh trồng rau. Chu vi miếng trồng ngô vội vàng 4 lần chu vi miếng trồng rau. Tính diện tích s thửa ruộng ban đầu, biết chiều rộng của chính nó là 5 mét.
Bài giải
Diện tích mảnh trồng ngô vội 6 lần diện tích s mảnh trồng rau mà lại hai mảnh bao gồm chung một cạnh buộc phải cạnh sót lại của mảnh trồng ngô vội 6 lần cạnh còn sót lại của miếng trồng rau. Gọi cạnh sót lại của mảnh trồng rau xanh là a thì cạnh sót lại của mảnh trồng ngô là a x 6. Vì chu vi mảnh trồng ngô (P1) cấp 4 lần chu vi mảnh trồng rau củ (P2) yêu cầu nửa chu vi miếng trồng ngô vội 4 lần nửa chu vi mảnh trồng rau.
Nửa chu vi miếng trồng ngô rộng nửa chu vi miếng trồng rau củ là :
a x 6 + 5 - (a + 5) = 5 x a.
Ta gồm sơ đồ gia dụng :
Độ nhiều năm cạnh còn lại của miếng trồng rau xanh là : 5 x 3 : (5 x a - 3 x a) = 7,5 (m)
Độ nhiều năm cạnh còn sót lại của mảnh trồng ngô là : 7,5 x 6 = 45 (m)
Diện tích thửa ruộng ban đầu là : (7,5 + 4,5) x 5 = 262,5 (m2)
Bài 16: Tôi đi bộ từ trường về nhà với vận tốc 5 km/giờ. Về đến nhà mau chóng tôi đánh đấm xe mang lại bưu điện với gia tốc 15 km/giờ. Hiểu được quãng đường từ công ty tới trường ngắn thêm một đoạn quãng mặt đường từ nhà đến bưu năng lượng điện 3 km. Tổng thời hạn tôi đi sóng ngắn từ trường về nhà với từ nhà mang đến bưu điện là 1 trong những giờ 32 phút. Các bạn hãy tính quãng mặt đường từ bên tôi mang đến trường.
Bài giải
Thời gian nhằm đi 3 km bằng xe đạp là : 3 : 15 = 0,2 (giờ)
Đổi : 0,2 giờ đồng hồ = 12 phút.
Nếu giảm 3 km quãng con đường từ nhà mang đến bưu điện thì thời gian đi cả nhì quãng con đường từ nhà cho trường với từ nhà mang lại bưu năng lượng điện (đã bớt 3 km) là :
1 tiếng 32 phút - 12 phút = 1 giờ 20 phút = 80 phút.
Vận tốc đi xe đạp gấp vận tốc quốc bộ là : 15 : 5 = 3 (lần)
Khi quãng đường không đổi, gia tốc tỉ lệ nghịch với thời gian nên thời gian đi tự nhà cho trường gấp 3 lần thời gian đi từ bỏ nhà cho thư viện (khi đã tiết kiệm hơn 3 km). Vậy :
Thời gian đi từ nhà cho trường là : 80 : (1 + 3) x 3 = 60 (phút); 60 phút = 1 giờ
Quãng đường từ nhà mang đến trường là : 1 x 5 = 5 (km)
Bài 17: Cho phân số:
a) có thể xóa đi vào tử số và chủng loại số đầy đủ số nào mà giá trị của phân số vẫn không biến hóa không ?
b) trường hợp ta thêm số 2004 vào mẫu mã số thì đề xuất thêm số tự nhiên và thoải mái nào vào tử số để phân số không thay đổi ?
Bài giải
=

a) Để giá trị của phân số không thay đổi thì ta nên xóa những số ở mẫu mã mà tổng của chính nó gấp 6 lần tổng của không ít số xóa đi sinh hoạt tử. Lúc ấy tổng những số còn lại ở mẫu cũng gấp 6 lần tổng các số còn lại ở tử. Vị vậy đổi vai trò những số bị xóa với những số sót lại ở tử và mẫu thì ta sẽ sở hữu thêm cách thực hiện xóa.
Có vô số phương pháp xóa, ví dụ:
Số những số bị xóa sinh sống mẫu tăng dần và tổng phân tách hết mang đến 6: mẫu mã xóa 12 thì tử xóa 2 ; mẫu xóa 18 thì tử xóa 3 hoặc xóa 1, 2 ; chủng loại xóa 24 hoặc xóa 11, 13 thì tử xóa 4 hoặc xóa 1, 3 ; chủng loại xóa 12, 18 hoặc 13, 17 hoặc 14, 16 thì tử xóa 5 hoặc 2, 3 hoặc 1, 4 ; mẫu mã xóa 12, 24 hoặc 11, 25 hoặc 13, 23 hoặc 14, 22 hoặc 15, 21 hoặc 16, trăng tròn hoặc 17, 19 thì tử xóa 6 hoặc 1, 5 hoặc 2, 4 hoặc 1, 2, 3 ; mẫu mã xóa 18, 24 hoặc 17, 25 hoặc 19, 23 hoặc 20, 22 hoặc 11, 13, 18 hoặc 12, 13, 17 hoặc 11, 14, 17 hoặc 11, 15, 16 hoặc 12, 14, 16 hoặc 13, 14, 15 thì tử xóa 7 hoặc 1, 6 hoặc 2, 5 hoặc 3, 4 hoặc 1, 2, 4 ; ...
b) Để cực hiếm phân số ko đổi, ta thêm một trong những nào kia vào tử bởi 1/6 số tiếp tế mẫu. Vậy nếu thêm 2004 vào mẫu thì số buộc phải thêm vào tử là :
2004 : 6 = 334.
Bài 18: fan ta mang tích những số tự nhiên liên tiếp từ 1 mang đến 30 để chia cho 1000000. Các bạn hãy cho thấy :
1) Phép chia bao gồm dư không ?
2) mến là một số tự nhiên bao gồm chữ số tận thuộc là từng nào ?
Bài giải :
Xét tích A = 1 x 2 x 3 x ... X 29 x 30, trong các số ấy các quá số phân tách hết mang lại 5 là 5, 10, 15, 20, 25, 30 ; mà lại 25 = 5 x 5 vì đó rất có thể coi là tất cả 7 thừa số phân tách hết mang lại 5. Mỗi thừa số này nhân với một vài chẵn cho ta một số có tận thuộc là số 0. Vào tích A có những thừa số là số chẵn cùng không phân tách hết cho 5 là : 2, 4, 6, 8, 12, . . . , 26, 28 (có 12 số). Như đồ trong tích A có tối thiểu 7 cặp số tất cả tích tận thuộc là 0, vì vậy tích A bao gồm tận thuộc là 7 chữ số 0.
Số 1 000 000 có tận cùng là 6 chữ số 0 cần A phân tách hết cho 1 000 000 và thương là số thoải mái và tự nhiên có tận cùng là chữ số 0.
Bài 19: Ba chúng ta Toán, Tuổi và Thơ có một số trong những vở. Nếu mang 40% số vở của Toán chia đều cho Tuổi cùng Thơ thì số vở của ba bạn bằng nhau. Dẫu vậy nếu Toán ngắn hơn 5 quyển thì số vở của Toán bằng tổng số vở của Tuổi với Thơ. Hỏi mỗi các bạn có từng nào quyển vở ?
Bài giải
Đổi 40% = 2/5.
Nếu đem 2/5 số vở của Toán chia các cho Tuổi với Thơ thì mỗi bạn Tuổi giỏi Thơ các được thêm 2/5 : 2 = 1 tháng 5 (số vở của Toán)
Số vở còn lại của Toán sau thời điểm cho là :
1 - 2/5 = 3/5 (số vở của Toán)
Do đó ban đầu Tuổi hay Thơ có số vở là :
3/5 - 1/5 = 2/5 (số vở của Toán)
Tổng số vở của Tuổi và Thơ lúc đầu là :
2/5 x 2 = 4/5 (số vở của Toán)
Mặt không giống theo đề bài nếu Toán bớt đi 5 quyển thì số vở của Toán bằng tổng số vở của Tuổi với Thơ, do đó 5 quyển ứng với : 1 - 4/5 = 1/5 (số vở của Toán)
Số vở của Toán là : 5 : 1 tháng 5 = 25 (quyển)
Số vở của Tuổi hay Thơ là : 25 x 2/5 = 10 (quyển)
Bài đôi mươi : hai số tự nhiên và thoải mái A với B, biết A 2)
Bài 27: các bạn hãy cắt một hình vuông có diện tích s bằng 5/8 diện tích của một tờ bìa hình vuông cho trước.
Bài giải:
Chia cạnh tấm bìa hình vuông vắn cho trước làm 4 phần đều bằng nhau (bằng cách gấp đôi liên tiếp). Tiếp nối cắt theo những đường AB, BC, CD, DA. Những miếng bìa AMB, BNC, CPD, DQA xếp trùng khít lên nhau đề nghị AB = BC = CD = domain authority (có thể kiểm tra bởi thước đo). Dùng êke kiểm tra những góc của tấm bìa ABCD ta thấy những góc là vuông.
Nếu kẻ bởi bút chì những đường phân tách tấm bìa ban đầu thành rất nhiều ô vuông như hình mẫu vẽ thì ta có thể thấy
+ diện tích tấm bìa MNPQ là 16 ô vuông (ghép 2 hình tam giác với nhau thì được hình chữ nhật tất cả 3 hình vuông).
Do đó diện tích hình vuông ABCD là 16 – 6 = 10 (ô vuông) nên diện tích s ô vuông ABCD bởi 10 / 16 = 5 / 8 diện tích tấm bìa ban đầu.
Bài 28: Một mảnh đất nền hình chữ nhật được chia thành 4 hình chữ nhật nhỏ tuổi hơn có diện tích được ghi như hình vẽ. Các bạn có biết diện tích hình chữ nhật còn lại có diện tích s là bao nhiêu hay không?
Bài giải
Hai hình chữ nhật AMOP với MBQO có chiều rộng đều bằng nhau và có diện tích hình MBQO cấp 3 lần diện tích s hình AMOP (24 : 8 = 3 (lần)), vì thế chiều dài hình chữ nhật MBQO cấp 3 lần chiều dài hình chữ nhật AMOP (OQ = PO x 3). (1)
Hai hình chữ nhật POND với OQCN tất cả chiều rộng cân nhau và bao gồm chiều dài hình OQCN cấp 3 lần chiều dài hình POND (1). Bởi vì đó diện tích s hình OQCN cấp 3 lần diện tích s hình POND.
Vậy diện tích hình chữ nhật OQCD là : 16 x 3 = 48 (cm2).
Xem thêm: Sách Bài 12 Toán 6 Chân Trời Sáng Tạo Toán 6 Tập 1, Sách Bài Tập Toán Lớp 6 Bài 12
Bài 29: Cho A = 2004 x 2004 x ... X 2004 (A bao gồm 2003 vượt số) và
B = 2003 x 2003 x ... X 2003 (B tất cả 2004 vượt số).
Hãy cho thấy thêm A + B có chia hết mang đến 5 giỏi không? bởi vì sao?
Bài giải
A = (2004 x 2004 x ... X 2004) x 2004 = C x 2004 (C bao gồm 2002 thừa số 2004). C gồm tận cùng là 6 nhân cùng với 2004 cần A có tận cùng là 4 (vì 6 x 4 = 24).
B = 2003 x 2003 x ... X 2003 (gồm 2004 thừa số) = (2003 x 2003 x 2003 x 2003) x ... X (2003 x 2003 x 2003 x 2003). Vị 2004 : 4 = 501 (nhòm) cần B có 501 nhóm, từng nhóm tất cả 4 vượt số 2003. Tận thuộc của từng nhóm là một trong (vì 3 x 3 = 9 ; 9 x 3 = 27 ; 27 x 3 = 81).
Vậy tận cùng của A + B là 4 + 1 = 5. Vì vậy A + B phân tách hết cho 5.
Bài 30: Biết rằng số A chỉ viết bởi những chữ số 9. Hãy tra cứu số trường đoản cú nhiên nhỏ dại nhất cơ mà cộng số này với A ta được số phân chia hết mang lại 45.
Bài giải
Cách 1: A chỉ viết bởi các chữ số 9 nên:
Vậy A phân tách cho 45 dư 9. Một số bé dại nhất mà cộng với A và để được số phân chia hết mang đến 45 thì số đó cộng với 9 phải bằng 45.
Vậy số sẽ là : 45 - 9 = 36.
Cách 2: hotline số tự nhiên nhỏ dại nhất cộng vào A là m. Ta gồm A + m là số chia hết cho 45 hay chia hết mang đến 5 và 9 (vì 5 x 9 = 45 ; 5 với 9 ko cùng phân tách hết cho một số số nào kia khác 1). Bởi vì A viết bởi những chữ số 9 buộc phải A phân tách hết cho 9, cho nên vì thế m phân chia hết cho 9. A + m chia hết mang đến 5 khi A + m tất cả tận thuộc là 0 hoặc 5 cơ mà A có tận thuộc là 9 phải m gồm tận cùng là 1 hoặc 6. Số nhỏ dại nhất tất cả tận cùng là 1 hoặc 6 mà phân tách hết mang đến 9 là 36.
Bài 31: Tham gia SEA Games 22 môn soccer nam vòng sơ loại ở bảng B tất cả bốn đội tranh tài theo thể thức đấu vòng tròn một lượt cùng tính điểm theo lý lẽ hiện hành. Kết thúc vòng loại, tổng thể điểm những đội sinh hoạt bảng B là 17 điểm. Hỏi ngơi nghỉ bảng B môn bóng đá nam bao gồm mấy trận hòa?
Bài giải
Bảng B tất cả 4 đội thi đấu vòng tròn cần số cuộc chiến là: 4 x 3 : 2 = 6 (trận)
Mỗi trận thắng thì đội thắng được 3 điểm đội lose thì được 0 điểm bắt buộc tổng số điểm là: 3 + 0 = 3 (điểm).
Mỗi trận hòa thì từng đội được một điểm bắt buộc tổng số điểm là: 1 + 1 = 2 (điểm).
Cách 1: trả sử 6 trận phần đông thắng thì tổng cộng điểm là: 6 x 3 = 18 (điểm).
Số điểm dôi ra là: 18 - 17 = 1 (điểm).
Sở dĩ dôi ra một điểm là vì chưng một trận chiến hạ hơn một trận hòa là: 3 - 2 = 1 (điểm). Vậy số trận hòa là: 1 : 1 = 1 (trận)
Cách 2: trả sử 6 trận các hòa thì số điểm làm việc bảng B là: 6 x 2 = 12 (điểm).
Số điểm ngơi nghỉ bảng B bị hụt đi: 17 - 12 = 5 (điểm).
Sở dĩ bị hụt đi 5 điểm là vì mỗi trận hòa kém mỗi trận win là: 3 - 2 = 1 (điểm). Vậy số trận chiến hạ là: 5 : 1 = 5 (trận).
Số trận hòa là: 6 - 5 = 1 (trận).
Bài 32: Một shop có tía thùng A, B, C để đựng dầu. Trong đó thùng A đựng đầy dầu còn thùng B với C thì sẽ để không. Nếu rót dầu ở thùng A vào đầy thùng B thì thùng A còn 2/5 thùng. Nếu bỏ dầu ở thùng A vào đầy thùng C thì thùng A còn 5/9 thùng. Muốn đổ dầu ngơi nghỉ thùng A vào đầy cả thùng B và thùng C thì nên thêm 4 lít nữa. Hỏi từng thùng chứa từng nào lít dầu?
Bài giải
So với thùng A thì thùng B rất có thể chứa được số dầu là: 1 - 2/5 = 3/5 (thùng A).
Thùng C có thể chứa được số dầu là: 1 - 5/9 = 4/9 (thùng A).
Cả 2 thùng có thể chứa được số dầu nhiều hơn thế nữa thùng A là:
(3/5 + 4/9) - 1 = 2/45 (thùng A).
2/45 số dầu thùng A chính là 4 lít dầu.
Do đó số dầu nghỉ ngơi thùng A là: 4 : 2/45 = 90 (lít).
Thùng B hoàn toàn có thể chứa được là: 90 x 3/5 = 54 (lít).
Thùng C hoàn toàn có thể chứa được là: 90 x 4/9 = 40 (lít).
Bài 33. Hải hỏi Dương: “Anh buộc phải hơn 30 tuổi phải không ?”. Anh Dương nói : “Sao già nạm ! ví như tuổi của anh ấy nhân với 6 thì được số có bố chữ số, nhị chữ số cuối đó là tuổi anh”. Các bạn cùng Hải tính tuổi của anh Dương nhé.
Bài giải:
Cách 1: Tuổi của anh ấy Dương không thật 30, khi nhân với 6 sẽ là số có 3 chữ số. Vậy chữ số hàng ngàn của tích là 1. Nhị chữ số cuối của số tất cả 3 chữ số đó là tuổi anh. Vậy tuổi anh Dương khi nhân cùng với 6 rộng tuổi anh Dương là 100 tuổi. Ta gồm sơ đồ:
Tuổi của anh Dương là : 100 : (6 - 1) = 20 (tuổi)
Cách 2: call tuổi của anh ý Dương là ab (a > 0, a, b là chữ số)
Vì ab không thật 30 nên những khi nhân với 6 sẽ tiến hành số có bố chữ số nhưng chữ số hàng trăm là 1. Ta gồm phép tính:
Vậy tuổi của anh ấy Dương là 20.
Bài 34: ở SEA Games 22 vừa qua, chị Nguyễn Thị Tĩnh giành Huy chương tiến thưởng ở cự li 200 m. Biết rằng chị chạy 200 m chỉ mất

Bài giải:
Kết quả thi đấu ở SEA Games 22 đã cho biết : Chị Nguyễn Thị Tĩnh chạy cự li 400 m với thời gian là 51 giây 82.
Nhận xét : dụng tâm của người ra đề là muốn các bạn giải toán cân nhắc tính thực tiễn của đề toán. Đề toán phát âm lên cứ như thể loại toán về đối sánh tương quan tỉ lệ thuận. Đa số các bạn đều tưởng như vậy đề nghị đã giải sai, ra đáp số là

Bài 35: Hãy mày mò “bí mật” của hình vuông rồi điền nốt tư số tự nhiên còn thiếu hụt vào ô trống.
Bài giải :
“Bí mật” của hình vuông là tổng các số hàng ngang, sản phẩm dọc với đường chéo cánh của hình vuông vắn đều bởi 34 (các bạn tự kiểm soát lại).
Gọi các số đề nghị tìm ở 4 góc của hình vuông vắn là a, b, c, d. ở sản phẩm ngang đầu tiên, ta có : a + 3 + 2 + b = 34, từ kia a + b = 34 - 5 = 29 (1).
Ở cột dọc trước tiên ta bao gồm : a + 5 + 9 + d = 34, từ đó a + d = 34 - 14 = 20 (2).
Từ (1) và (2) ta gồm : a + b - (a + d) = 29 - đôi mươi = 9 giỏi b - d = 9 (3).
Ở một con đường chéo, ta lại sở hữu : b + 6 + 11 + d = 34, từ kia b + d = 34 - 17 = 17 (4).
Từ (3) và (4) ta có : (b - d) + (b + d) = 9 + 17 tuyệt b + b = 26 ; b = 13.
Vì b + d = 17 đề nghị d = 17 - 13 = 4.
Vì a + b = 29 buộc phải a = 29 - 13 = 16.
Ở đường chéo cánh thứ hai, ta bao gồm a + 10 + 7 + c = 34 hay a + c = 34 - 17 = 17.
Từ đó c = 17 - 16 = 1. Nuốm a, b, c, d bằng các số vừa tìm kiếm được ta có hình vuông vắn sau:
Nhận xét : hình vuông trên hotline là hình vuông vắn kì ảo (hoặc ma phương) cung cấp 4. Bạn ta đã nhận thức thấy nó lần trước tiên trong bạn dạng khắc của họa sỹ Đuy-rơ năm 1514. Các chúng ta có thể thấy : Tổng tư số trong tứ ô ở bốn góc cũng bởi 34.
Bài 36: chúng ta cũng có thể cắt hình này :
thành 16 hình: bạn hãy nói rõ bí quyết cắt nhé !
Bài giải:
Tổng số ô vuông là : 8 x 8 = 64 (ô)
Khi ta cắt hình vuông thuở đầu thành những phần nhỏ tuổi (hình chữ T), mỗi phần tất cả 4 ô vuông thì sẽ tiến hành số hình là : 64 : 4 = 16 (hình)
Ta có thể cắt theo rất nhiều cách thức khác nhau:
Trên đó là 500 câu hỏi có giải thuật ôn thi học sinh giỏi, ôn thi vào lớp 6 cho các em học viên tham khảo ôn tập, củng nuốm kiến thức chuẩn bị cho những kì thi đạt tác dụng cao.
Đồng hành cùng con trong quy trình học tập, ba bà bầu đã nắm rõ các dạng toán lớp 5 với phương pháp giải từng bài? Để con có một hành trang vững vàng, nội dung bài viết sau phía trên toancapba.com đã tổng hợp cụ thể các kỹ năng và kiến thức toán lớp 5 cùng những ví dụ và biện pháp giải để phụ huynh có thể cùng bé ôn tập lại một cách chuyên nghiệp hóa và dễ dàng.
Tổng hợp những dạng kỹ năng lớp 5
Để giúp phụ huynh và các con dễ dãi củng thay lại kiến thức lớp 5, toancapba.com liệt kê 8 dạng Toán chính mà các em được học tập trong chương trình giáo dục và đào tạo lớp 5 như:
Dạng 1: Trung bình cộngDạng 2: Tìm hai số khi biết tổng và hiệu của nhị số đóDạng 3: Tìm nhì số lúc biết tổng và tỉ của hai số đóDạng 4: Tìm nhị số khi biết hiệu và tỉ của nhì số đóDạng 5: quan lại hệ tỉ lệDạng 6: Tỉ số phần trăm
Dạng 7: Chuyển động đều
Dạng 8: Hình học

Các dạng toán lớp 5 và phương pháp giải
Chi tiết rộng về các dạng toán, phụ huynh hoàn toàn có thể tham khảo một số trong những ví dụ sau:
1. Dạng toán trung bình cộng
Học sinh vẫn được ban đầu tiếp xúc với kiến thức toán trung bình cộng ở lớp bốn, và đi học năm, con kiến thức cùng bài triệu tập bình được xen kẽ với đa số kiến thức cùng dạng bài bác tập không giống nhau. Yêu thương cầu học viên nắm vững những kiến thức khi có tác dụng bài cũng như thuần thục các dạng bài xích tập về mức độ vừa phải cộng.
Bài tập ví dụ:
Câu 1: Tính trung bình cộng của các số sau: 25, 37, 41.
Lời giải:
Trung bình cộng của 3 số trên là: (25 + 39 + 41) : 3 = 35
Câu 2: Một xe pháo máy đi từ Hà Nội tới Hải Phòng mất 3 giờ. Giờ đầu tiên xe máy đi với tốc độ 37km/h. Giờ thứ 2, xe máy đi với tốc độ to hơn là 40km/h với Quãng đường còn lại xe pháo máy đi với vận tốc 50km/h.
Tính vận tốc trung bình của xe pháo máy là bao nhiêu Quãng đường đi từ Hà Nội đến Hải Phòng của xe vật dụng hết từng nào km?Lời giải:
Ta bao gồm vận tốc trung bình xe pháo máy đi là:(36 + 40 + 50) : 3 = 42 (km/h)
Quãng đường từ thành phố hà nội đến tp. Hải phòng xe máy đi không còn số km là:42 x 3 = 126 (km)
Đáp số: 42 (km/h), 126 (km)

2. Dạng tìm 2 số lúc biết tổng cùng hiệu của 2 số đó
Khi tổng hợp những dạng toán lớp 5 và cách thức giải ba chị em nên quan trọng đặc biệt quan trung khu tới dạng bài bác tìm nhì số biết tổng và hiệu của chúng.
Các dạng bài xích tập trong phần loài kiến thức này yên cầu học sinh yêu cầu nắm vững năng lực vẽ biểu vật dụng đoạn thẳng. Học tập sinh cần phải biết cách diễn đạt và cầm tắt đề bài dưới dạng biểu vật dụng đường.
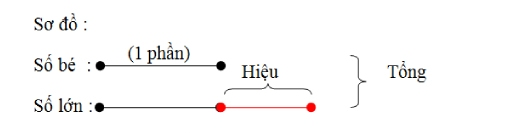
Bài tập
Câu 1: Tổng số tuổi chị cùng em hiện nay là 40 tuổi. Tuổi chị bằng 5/8 tổng số tuổi cả 2. Biết tuổi em ít rộng chị 2 phần. Hỏi số tuổi của 2 chị em hiện nay.
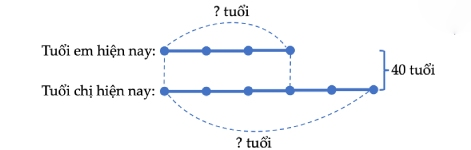
Lời giải:
Ta bao gồm số tuổi của em hiện ni là:
40 : 8 x 3 = 15 (tuổi)
Số tuổi của chị hiện nay là:
40 -15 = 25 (tuổi)
Câu 2: đến hai số có tổng là 96. Trong đó số bé chỉ bằng 3/8 tổng của nhị số còn số lớn nhiều hơn 2 lần số bé. Tìm nhị số đó.
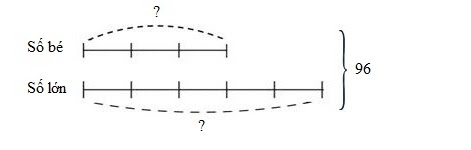
Lời giải
Ta có số bé là:
96 : 8 x 3 = 36 (đơn vị)
Số lớn là:
96 – 36 = 60 (đơn vị)
3. Dạng tìm kiếm 2 số khi biết tổng với tỉ số của 2 số đó
Khi ôn tập Toán lớp 5 dạng bài tập này, chúng ta cần lưu lại ý tương tự như dạng 2. Học sinh cần biết cách vẽ sơ đồ đạn thẳng từ dữ liệu đè bài mang lại trước. Ngoài ra các bạn học sinh cần nắm chắc ôn lại kiến thức về tỉ số.
Bài tập
Câu 1: Lớp 5B có tất cả là 35 bạn học sinh. Vào đó tỉ số giữa học sinh nam cùng học sinh nữ là 3/4. Hỏi lớp 5B có từng nào bạn học sinh nam giới và bao nhiêu bạn học sinh nữ?
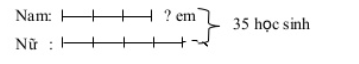
Ta bao gồm tổng số phần bằng nhau là:
3 + 4 = 7 (phần)
Số học sinh phái nam của lớp 5B là:
35 : 7 x 3 = 15 (học sinh)
Số học sinh nữ của lớp 5B là:
35 -15 =20 (học sinh)
4. Dạng toán tìm 2 số lúc biết hiệu với tỉ số của 2 số đó
Tổng hợp các dạng toán lớp 5 và phương pháp giải phụ huynh tất yêu liệt kê thiếu thốn dạng toán tra cứu 2 số khi biết hiệu và tỉ số của 2 số đó. Cũng tương tự yêu cầu của dạng 2 và dạng 3 sống dạng câu hỏi tìm 2 số khi biết hiệu cùng tỉ số 2 số nhỏ nhắn cần thành thạo bí quyết phân tích với vẽ sơ thứ đoạn thẳng.
Bài tập
Câu 1: Tỉ số hoa của người sử dụng Lan so với Hằng là ⅖ bông. Được biết, số hoa của bạn Lan giành được ít hơn cố hoa của Hằng là 15 bông. Hỏi số hoa mỗi bạn đã có.
Ta gồm hiệu số phần bằng nhau là:
5 -2 = 3 (phần)
Số hoa bạn Lan có là:
15 : 3 x 2 = 10 (bông)
Số hoa bạn Hằng có là:
10 + 15 =25 (bông)
5. Dạng toán quan hệ giới tính tỉ lệ
Trong quy trình ôn tập môn toán lớp 5, dạng toán về quan hệ tỉ lệ là một trong dạng toán mới mà những em được làm quen. Khác với 4 dạng Toán trên các được xúc tiếp từ lớp 4 thì đối với dạng toán tỉ lệ, học sinh nên biết cách rút về đối chọi vị, kiếm tìm mối tương tác giữa những đại lượng trong bài toán và search tỉ số.

Bài tập
Câu 1: Một xe cộ máy vào 2 giờ đi được 40 km. Hỏi vào 4 giờ xe máy đã đi được từng nào km?
Tóm tắt
Xe sản phẩm đi vào 2 giờ : 40 kmXe trang bị đi vào 4 giờ: ? km
Lời giải
1 giờ xe máy đi được là:
40 : 2 = 20 (km)
4 giờ xe cộ máy đi được là:
20 x 4 = 80 (km)
Đáp số: 80km
Câu 2: Để vệ sinh ngừng lớp học cần cho tới 3 bạn học sinh làm vào 9 phút. Nếu muốn quét lớp học dứt nhanh chóng trong tầm 5 phút cần bao nhiêu bạn học sinh?
Tóm tắt
9 phút : 3 bạn học sinh5 phút : ? học sinhLời giải
Muốn quét lớp vào 5 phút xong, ta cần số học sinh là: 9 : 3 x 5 = 15 bạn học sinh.
Đáp số: 15 bạn học sinh

6. Dạng toán tỉ số phần trăm
Để làm xuất sắc các câu hỏi về tỉ số phần trăm đòi hỏi học sinh cần nắm chắc định hướng và nắm rõ thực hành các kiến thức về tỉ số.
Bài tập
Câu 1: Lớp 5A có 40 bạn học sinh vào đó có 18 bạn nam và 22 bạn nữ. Hỏi:
Tỉ số thân số bạn phái nam và bạn nữ. Tỉ số giữa số bạn nữ và bạn nam. Tỉ số thân số bạn nữ và cả lớp. Tỉ số giữa số bạn nam và cả lớp.Lời giải:
Tỉ số của số bạn phái mạnh và bạn nữ là: 18 : 22 = 9/11 Tỉ số của số bạn nữ và bạn phái mạnh là: 22 : 18 = 11/9 Tỉ số số bạn nữ và cả lớp là : 22 : 40 = 11/20 Tỉ số số bạn phái nam và cả lớp là: 18 : 40 = 9/207. Dạng toán hoạt động đều
Trong ôn tập toán lớp 5, dạng toán hoạt động đều yêu cầu học viên cần nên nắm chắc những công thức và những đơn vị tính vận tốc.
Công thức : S = V x T. Trong đó:
S là quãng đườngV là vận tốc
T là thời gian
Các đối chọi vị vận tốc là: km/h, m/phút, m/s,…
Bài tập
Câu 1: Bác tứ chạy 20m mất khoảng tầm 5 phút. Tính vận tốc chạy của bác Tư.
Lời giải:
Vật tốc chạy của bác bốn là: đôi mươi : 5 = 4m/phút
Đáp số: 4m/phút
Câu 2: Một xe xe hơi đi với vận tốc là 45km/h. Hỏi trong thời gian 5 giờ xe hơi chạy hết từng nào km?
Lời giải
Trong 5 giờ xe hơi chạy được quãng đường số km là: 45 x 5 = 225 km
Đáp số: 225 km
8. Dạng toán hình học
Khối lớp 5 có nhiều kiến thức hình học và cực kỳ khó. Cùng với kỹ năng hình học lớp 5 học sinh cần phải biết cách tính chu vi, diện tích hình tam giác, hình tròn, hình thang và tính chu vi, diện tích s toàn phần, thể tích hình lập phương.
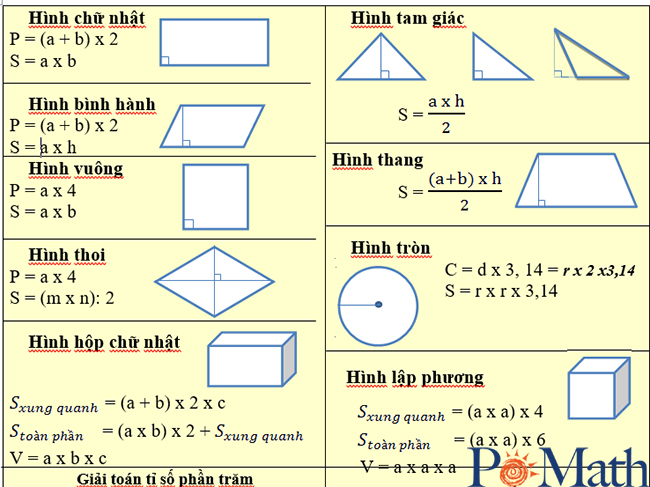
Bài tập
Câu 1: Một khúc mộc hình hộp chữ nhật có chiều dài 18cm. Chiều rộng khúc mộc là 15cm. Chiều cao khúc gỗ là 4 cm.
Yêu cầu tính diện tích xung quang, diện tích toàn phần của khúc gỗ đó. Tính diện tích bao phủ và diện tích toàn phần của khối hình hộp chữ nhật lúc xếp chồng 6 khúc gỗ thành 2 hàng bằng nhau.Lời giải:
diện tích s xung xung quanh của khúc gỗ đó là:(18 + 15) x 2 x 4 = 184 (cm2)
Diện tích đáy khúc mộc là:
18 x 15 = 270 (cm)
Diện tích toàn phần của khúc gỗ kia là:
184 + 270 x 2 = 724 (cm2)
Khi xếp ông chồng 6 khúc gỗ thành 2 hàng bằng nhau ta được mỗi hàng tất cả 3 khúc mộc xếp ông xã lên nhau.
Chiều rộng của khối hình vỏ hộp chữ nhật được làm bằng gỗ là: 15×2 = 30 (cm)
Chiều cao của khối hình vỏ hộp chữ nhật bằng gỗ là: 4×3 = 12 (cm)
Diện tích bao quanh của khối hình vỏ hộp chữ nhật bằng gỗ là:
2 x 12 x (30 + 18)= 1152 (cm2)
Diện tích toàn phần của khối hình hộp chữ nhật bởi gỗ:
1152 + (270 x 2) x 2= 2232 (cm2)
Lời kết
Trên là tổng thích hợp các dạng toán lớp 5 cùng phương pháp giải bởi toancapba.com tổng hợp và biên soạn. Hy vọng rằng với ngôn từ trên sẽ giúp đỡ phụ huynh và các bé xíu có bí quyết củng nắm và ôn tập giỏi kiến thức toán học tập lớp 5.









