a) Đường trực tiếp (∆) là đường thẳng vuông góc phổ biến của hai đường thẳng (a) cùng (b) nếu như (∆) vuông góc với (a) với (∆) vuông góc với (b);
b) điện thoại tư vấn ((P)) là phương diện phẳng tuy nhiên song đối với cả hai mặt đường thẳng (a, b) chéo nhau. Khi ấy đường vuông góc tầm thường (∆) của (a) cùng (b) luôn luôn vuông góc cùng với ((P));
c) gọi (∆) là mặt đường vuông góc chung của hai tuyến phố thẳng chéo nhau (a) cùng (b) thì (∆) là giao tuyến của nhì mặt phẳng ((a, ∆)) với ((b, ∆));
d) Cho hai tuyến phố thẳng chéo nhau (a) và (b). Đường thẳng nào đi sang một điểm (M) trên (a) đồng thời giảm (b) trên (N) và vuông góc với (b) thì sẽ là đường vuông góc thông thường của (a) với (b);
e) Đường vuông góc bình thường (∆) của hai đường thẳng chéo nhau (a) và (b) phía trong mặt phẳng đựng đường này với vuông góc với mặt đường kia.
Bạn đang xem: Toán hình lớp 11 trang 119
Video gợi ý giải
Phương pháp giải - Xem bỏ ra tiết

Xét tính đúng sai của từng mệnh đề (có thể vẽ hình để sở hữu cái nhìn trực quan tiền hơn).
Quảng cáo

Lời giải bỏ ra tiết
a) Sai vày thiếu điều kiện (Delta ) cắt cả a và b.
b) Đúng.
c) Đúng.
d) Sai vì chưng thiếu đk đường thẳng đó cũng phải vuông góc cùng với a.
e) Sai vì nếu điều ấy xảy ra thì a với b vuông góc mà lại giả thiết chưa cho a vuông góc b.
Loigiaihay.com


Chia sẻ
Bình chọn:
3.7 trên 18 phiếu
Bài tiếp sau

Luyện bài bác Tập Trắc nghiệm Toán 11 - xem ngay
Báo lỗi - Góp ý
2K7 thâm nhập ngay group nhằm nhận tin tức thi cử, tư liệu miễn phí, thảo luận học tập nhé!

 |  |  |  |
 |  |  |  |
TẢI app ĐỂ coi OFFLINE
Bài giải bắt đầu nhất
× Góp ý mang lại loigiaihay.com
Hãy viết cụ thể giúp Loigiaihay.com
Vui lòng nhằm lại tin tức để ad hoàn toàn có thể liên hệ với em nhé!
Gửi góp ý Hủy bỏ
× Báo lỗi góp ý
Vấn đề em gặp mặt phải là gì ?
Sai chủ yếu tả
Giải cực nhọc hiểu
Giải sai
Lỗi khác
Hãy viết chi tiết giúp Loigiaihay.com
giữ hộ góp ý Hủy bỏ
× Báo lỗi
Cảm ơn các bạn đã áp dụng Loigiaihay.com. Đội ngũ cô giáo cần cải thiện điều gì để chúng ta cho nội dung bài viết này 5* vậy?
Vui lòng nhằm lại thông tin để ad có thể liên hệ với em nhé!
Họ cùng tên:
nhờ cất hộ Hủy vứt
Liên hệ chính sách




Đăng cam kết để nhận giải thuật hay với tài liệu miễn phí
Cho phép loigiaihay.com gởi các thông báo đến bạn để nhận ra các giải mã hay tương tự như tài liệu miễn phí.
Kiến Guru xin phép được gửi đến bạn đọc toàn bộ bài tập và chỉ dẫn giải bài tập toán 11 hình học làm việc trang 119 vào sách giáo khoa hình học tập 11. Ở trang 119 SGK hình học 11 có tổng cộng 6 bài bác , được phân dạng theo từng nấc độ cực nhọc dễ khác nhau. Nhằm mục tiêu mục đích cho học sinh ôn tập với tổng hợp các kiến thức cho bài “Khoảng Cách”thuộc vào chương 3:“Vectơ trong ko gian. Tình dục vuông góc trong ko gian”. Mời chúng ta đọc tham khảo
1. Gợi ý giải bài tập toán 11 hình học bài 1 trang 119 SGK
Trong toàn bộ các mệnh đề dưới đây mệnh đề như thế nào là đúng?
a) Đường trực tiếp Δ là mặt đường vuông góc phổ biến của hai đường thẳng a và b nếu Δ ⊥a và Δ ⊥b.
b) gọi (P) là mặt phẳng tuy nhiên song với tất cả hai đường thẳng a và b chéo nhau thì con đường vuông góc bình thường của a cùng b luôn luôn luôn vuông góc với (P).
c) call Δ là mặt đường vuông góc thông thường của hai đường thẳng chéo cánh nhau a với b thì Δ là giao đường của hai mặt phẳng (a, Δ) cùng (b, Δ).
d) Cho hai đường thẳng chéo nhau a cùng b. Đường thẳng như thế nào đi qua một điểm M bên trên a đồng thời giảm b trên N và vuông góc cùng với b thì sẽ là đường vuông góc phổ biến của a và b.
e) Đường vuông góc bình thường Δ của hai tuyến phố thẳng chéo cánh nhau a cùng b phía bên trong mặt phẳng cất đường này cùng vuông góc với con đường kia.
Hướng dẫn giải
a) Sai
Sửa lại: "Đường trực tiếp Δ là con đường thẳng vuông góc chung của hai tuyến phố thẳng chéo nhau a cùng b giả dụ Δ cắt cả a và b, đôi khi Δ ⊥ a với Δ ⊥ b"
b) Đúng
c) Đúng
d) Sai
Sửa lại: Đường thẳng đi qua M trên a cùng vuông góc với a, đồng thời cắt b trên N và vuông góc cùng với b thì chính là đường vuông góc bình thường của a với b.
e) Sai.
2. Lý giải giải bài bác tập toán 11 hình học bài 2 trang 119 SGK
Cho tứ diện S.ABC có đường thẳng SA vuông góc khía cạnh phẳng (ABC). điện thoại tư vấn H là trực trọng điểm của tam giác ABC , K là trực tâm của tam giác SBC.
Xem thêm: Cung Và Góc Lượng Giác: Lý Thuyết Và Các Dạng Toán 10 Độ Radian Sang Độ 10
a) chứng tỏ ba mặt đường thẳng AH, SK, BC đồng quy.
b) chứng tỏ đường thẳng SC vuông góc với mặt phẳng (BHK) . Đường thẳng HK vuông góc với khía cạnh phẳng (SBC).
c) xác minh đường vuông góc chung của BC với SA.
Hướng dẫn giải


Những kỹ năng cần để ý trong vấn đề :
+ nhì mặt phẳng thuộc vuông góc với khía cạnh phẳng thứ tía thì giao con đường của chúng (nếu có) cũng vuông góc với khía cạnh phẳng máy ba.
+ Đường vuông góc chung của hai tuyến phố thẳng chéo nhau a, b là đường thẳng cắt a, b và cùng vuông góc cùng với a, b.
3. Hướng dẫn giải bài tập toán hình lớp 11 bài 3 trang 119 SGK
Cho hình lập phương ABCD.A"B"C"D"cạnh a. Chứng tỏ rằng các khoảng cách từ những điểm B, C, D, A", B"và D"đến đường chéo cánh AC"đều bằng nhau. Tính khoảng cách đó.
Hướng dẫn giải

a) Ta có: ∆ ABC’ = ∆ C’CA = ∆ADC’=∆ AA’C’ =∆ C’B’A = ∆C’D’A (c.c.c)
Suy ra những đường cao hạ từ bỏ B; C; D; A’; B’; D’ xuống AC’ bằng nhau
( chú ý: các tam giác trên đều phải có chung cạnh AC’)
Gọi khoảng cách đó là h.
Ta có: CC’ = a;

ΔC’AC vuông tại C, tất cả hai cạnh góc vuông là CA với CC’. Áp dụng hệ thức về cạnh và con đường cao vào tam giác vuông ta có:
Ta có :
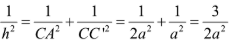
Suy ra : h =

4. Chỉ dẫn giải toán 11 hình học bài bác 4 trang 119 SGK
Có AB = a, BC = b, CC"= c lần lượt là các cạnh đã đến của hình vỏ hộp chữ nhật ABCD.A"B"C"D"
a) Tính khoảng cách từ B mang đến mặt phẳng (ACC"A").
b) Tính khoảng cách giữa hai đường thẳng BB"và AC".
Hướng dẫn giải

1. Ta gồm : AA’

AA’

Suy ra (ACC’A’)

Hai phương diện phẳng này vuông góc với nhau cà căt nhau theo giao tuyến AC phải nếu trường đoản cú B ta kẻ bh


Ta có :

Ta lại sở hữu BH.AC = BA.BC (=
Suy ra :

b) Ta có :CC’//BB’
Mà CC’

Nên d(BB’;AC’)=d(BB’;(ACC’A’)
=d(B;(ACC’A’)) = bảo hành =

5. Khuyên bảo giải bài xích tập toán hình 11 bài 5 trang 119 SGK
Cho hình lập phương ABCD.A"B"C"D"
a) chứng minh rằng B"D vuông góc với khía cạnh phẳng (BA"C")
b) Tính khoảng cách giữa khía cạnh phẳng (ACD") với mặt phẳng (BA"C")
c) Tính khoảng cách giữa hai tuyến đường thẳng BC" và CD"
Hướng dẫn giải
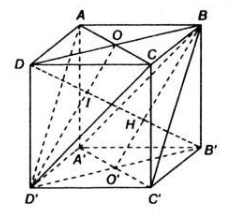

b) Xét tứ giác A’BCD’ có BC//A’D’ và BC = A’D’
=> tứ giác A’BCD’ là hình bình hành
=> BA’ // CD’ ( đặc điểm của hình bình hành)
Tương tự, tứ giác ABC’D’ là hình bình hành đề nghị BC’//AD’
Ta bao gồm

Gọi O với O’ là trọng tâm của ABCD và A’B’C’D’.
Gọi H với I theo lần lượt là trung ương của nhì tam giác gần như BA’C’ và ACD’.
* Xét ( BB’D’D)
Ta tất cả BO’// D’O đề xuất OI // HB
Vì : O là trung điểm BD
=> I là trung điểm của HD: IH = ID (1)
* Xét (BB’D’D)
Ta tất cả D’O// BO’ nên D’I // HO’
Vì : O’ là trung điểm của B’D’ đề nghị H là trung điểm B’I: HI = HB’ (2)

Từ (1) và (2) suy ra:
* Theo phần trên B"D ⊥ (BA"C) ⇒ IH ⊥ (BA"C)
Mà I ∈ (ACD") nên khoảng cách giữa nhị mp tuy vậy song (ACD’) và ( BA’C’) là độ dài đoạn IH.
Khi đó:


mà (BA’C’)//(ACD’)
Vậy d(BC’;CD’) = d((BA’C’);(ACD’)) =

6. Trả lời giải bài bác tập toán 11 hình học bài xích 6 trang 119 SGK
Chứng minh rằng nếu mặt đường thẳng nối trung điểm nhì cạnh AB và CD của tứ diện ABCD là mặt đường vuông góc chung của AB với CD thì AC = BD với AD = BC.
Hướng dẫn giải

Gọi I, K lần lượt là trung điểm của cạnh AB với CD
Qua K kẻ đường thẳng d // AB, bên trên d mang A", B" làm sao cho K là trung điểm của A"B" và
KA" = IA
* Xét tam giác CKB’ và DKA’ có:
KC= KD ( mang thiết)
KB’= KA’( cách dựng)
CKB"=A"KD( hai góc đối đỉnh )
=> ∆ CKB’ = ∆ DKA’ ( c.g.c)
=> B’C = A’D
*Xét tứ giác IBB’K tất cả IB= KB’ cùng IB // KB’ ( bí quyết dựng)
=> Tứ giác IBB’K là hình bình hành
=> BB’ // IK (1)
Chứng minh tương tự, ta có: AA’// IK (2)
Từ (1) và (2) suy ra: BB’// IK// AA’ (*)
Ta tất cả :

Lại có:IK ⊥ CK
=> IK ⊥ (CKB") (**)
Từ (*) cùng (**) suy ra BB" ⊥ (CKB") ; AA" ⊥ (CKB")
⇒ BB" ⊥ B"C; AA" ⊥ A"D
* Xét nhị tam giác vuông BCB’ cùng ADA’ có:
BB’ = AA’ (= IK)
CB’ = A’D (chứng minh trên)
=> ∆ BCB’ = ∆ ADA’ ( cạnh huyền –cạnh góc vuông)
=> BC= AD.
* chứng tỏ tương tự, AC = BD
Đây là tổng hợp hướng dẫn giải bài xích tập toán 11 hình học do Kiến Guru dành nhiều tâm tiết biên soạn. Muốn rằng sẽ cung ứng nhiều cho chính mình đọc trong quy trình học tập và làm bài tương tự như có thêm nguồn tài liệu để tham khảo và chuẩn bị cho quá trình ôn tập của chính mình nhé. Chúc chúng ta đọc ôn luyện và làm bài tập thường xuyên để có hiệu quả tốt một trong những kỳ chất vấn và các kỳ thi đặc trưng sắp tới.










