phương pháp toán hình 12 có tương đối nhiều các dạng bài, đôi lúc sẽ khiến bọn họ dễ nhầm lẫn. Đừng lo! bài viết chia sẻ đến cho chúng ta toàn bộ phương pháp toán 12 hình học, không chỉ giúp thuận tiện tổng phù hợp kiến thức, ngoài ra mang lại cục bộ kiến thức toán hình 12 rất đầy đủ đến mỗi học tập sinh.
1. Tổng hợp công thức toán hình 12 khối nhiều diện
Đến cùng với chương đầu tiên - khối đa diện, bạn được học về hình chóp tam giác, chóp tứ giác, hình hộp,... Chúng ta có thể hiểu rằng khối nhiều diện là phần không khí được giới hạn bởi hình nhiều diện, bao hàm cả hình nhiều diện đó. Ta sẽ có những bí quyết như sau:
1.1. Bí quyết toán hình 12 khối nhiều diện
Thể tích khối chóp áp dụng cho chóp tam giác cùng chóp tứ giác:
Công thức tính thể tích hình chóp được phát âm là một trong những phần ba diện tích dưới mặt đáy nhân cùng với chiều cao. Thể tích khối chóp tứ giác số đông và tam giác đều phải sở hữu cùng phổ biến công thức.
Bạn đang xem: Các công thức lớp 12 toán
Ta có thể tích khối chóp:

Trong đó:
S đáy:Diện tích mặt đáyh: Độ dài chiều caoThể tích khối chóp S.ABCD là:

1.2. Cách làm toán hình 12 khối lăng trụ
Hình lăng trụ có vài điểm lưu ý giống nhau, kia là:
Nằm trên 2 mặt phẳng tuy nhiên song với nhau và bao gồm hai đáy giống nhau.
Cạnh bên đôi một cân nhau và song song với nhau, những mặt bên là hình bình hành.


Thể tích khối lăng trụ được tính bằng công thức như sau:
V= S.h
Trong đó:
S là diện tích đáy.h là chiều cao.Lưu ý: Hình lăng trụ đứng bao gồm chiều cao chính là cạnh bên.
Ngoài ra, những em tất cả thể bài viết liên quan công thức tính thể tích khối lăng trụ tam giác đềuđể giải những bài tập về hình lăng trụ.
1.3.Thể tích hình vỏ hộp chữ nhật lớp 12
Hình vỏ hộp chữ nhật có các cạnh đáy lần lượt là a, b và chiều cao c, khi ấy thể tích hình vỏ hộp chữ nhật là V= a.b.c (a, b, c bao gồm cùng đối chọi vị).
Hình lập phương là dạng đặc biệt của hình vỏ hộp chữ nhật tất cả a = b = c. Do vậy thể tích hình lập phương được tính theo công thức: V = a3
1.4.Công thức toán hình 12 khối chóp cụt
Hình chóp cụt được quan niệm là một trong những phần của khối đa diện ở giữa dưới đáy và tiết diện cắt vày đáy của hình chóp với một mặt phẳng song song với đáy.
a) diện tích s xung quanh hình chóp cụtDiện tích bao phủ của hình chóp cụt là diện tích những mặt xung quanh, phần phủ bọc hình chóp cụt không bao gồm diện tích nhì đáy.
Diện tích hình chóp cụt đều được tính bằng bí quyết dưới đây:


Trong đó:
Sxq: diện tích s xung quanh.n: con số mặt bên.a, b: chiều lâu năm cạnh của 2 lòng trên với dưới của hình chóp cụt.h: chiều cao mặt bên.Công thức tính diện tích xung quanh của hình chóp cụt là tính diện tích s từng mặt mặt của hình chóp cụt theo cách làm tính diện tích hình thang bình thường, tiếp nối tính tổng diện tích của tất cả các hình cấu thành hình chóp cụt.
Nắm trọn toàn cục công thức và cách thức giải hồ hết dạng bài tập Toán hình 12 cùng với bộ bí quyết độc quyền của VUIHOC ngay!!!
b) công thức tính diện tích toàn phầnDiện tích toàn phần của hình chóp cụt được tính bằng tổng diện tích s 2 dưới mặt đáy và diện tích s xung xung quanh của hình chóp cụt đó.
Công thức:
Stp = Sxq + Sđáy lớn + Sđáy nhỏ
Trong đó:
Stp: diện tích s toàn phầnSxq: diện tích xung quanh
Sđáy lớn: diện tích đáy lớn
Sđáy nhỏ: diện tích s đáy nhỏc) Thể tích hình chóp cụt được tính bằng công thức
Công thức:
Trong đó:
V: thể tích hình chóp cụt.
S, S’ theo lần lượt là diện tích mặt dưới lớn và đáy nhỏ dại của hình chóp cụt.
Xem thêm: Giải Bài 4 Trang 101 Toán 12, Bài Tập 4 Trang 101 Sgk Giải Tích 12
h: độ cao (khoảng phương pháp giữa 2 dưới mặt đáy lớn với đáy nhỏ)
2. Công thức toán hình 12 hình nón
Có thể hiểu đơn giản, hình học tập có không khí ba chiều mà bề mặt phẳng và bề mặt cong phía lên bên trên là hình nón. Đầu nhọn của hình nón được call là đỉnh và bề mặt phẳng được call là đáy. Ta hoàn toàn có thể dễ dàng phát hiện những đồ vật dụng tất cả hình nón như loại nón lá, mũ sinh nhật,...
a) diện tích s xung xung quanh hình nón được xem bằng tích của số Pi (π) nhân với nửa đường kính đáy hình nón (r) rồi nhân với mặt đường sinh hình nón (l). Ta tất cả công thức:

Trong đó:
Sxq: là diện tích s xung quanh.π: là hằng sốr: là cung cấp kính dưới đáy hình nónl: con đường sinh của hình nón.b) diện tích s toàn phần hình nón được xem bằng diện tích xung xung quanh hình nón cùng với diện tích mặt đáy của hình nón.

Vì diện tích của mặt dưới là hình tròn nên ta vận dụng công thức tính diện tích hình tròn:

c) Để tính thể tích khốinón, ta vận dụng công thức sau:

Trong đó:
V: ký kết hiệu thể tích hình nónπ: = 3,14r: phân phối kính hình tròn đáy.h: là đường cao tính tự đỉnh hình nón xuống trung ương đường trònd) Tổng thích hợp một vài công thức mặt nón:
Đường cao: h=SO (hay còn gọi là trục của hình nón)
Bán kính đáy: r=OA=OB=OM
Đường sinh: l=SA=SB=SM
Góc ở đỉnh: ASB
Thiết diện qua trục SAB cân nặng tại S
Góc giữa dưới mặt đáy và mặt đường sinh: SAO=SBO=SMO
Chu vi đáy:

Diện tích đáy: Sđáy

PAS VUIHOC – GIẢI PHÁP ÔN LUYỆN CÁ NHÂN HÓA
Khóa học online ĐẦU TIÊN VÀ DUY NHẤT:
⭐Xây dựng lộ trình học tập từ mất gốc mang đến 27+
⭐Chọn thầy cô, lớp, môn học tập theo sở thích
⭐Tương tác trực tiếp hai chiều thuộc thầy cô
⭐ Học tới trường lại đến khi nào hiểu bài thì thôi
⭐Rèn tips tricks góp tăng tốc thời gian làm đề
⭐ khuyến mãi ngay full cỗ tài liệu chọn lọc trong quá trình học tập
Đăng cam kết học thử miễn giá tiền ngay!!
3. Công thức toán hình lớp 12 hình trụ
Hình được giới hạn bởi hai đường tròn có mặt trụ và đường kính bằng nhau được điện thoại tư vấn là hình trụ. Trong cách làm toán hình lớp 12, hình trụ cũng khá được tìm kiếm hơi nhiều, áp dụng cho cả dạng bài phức hợp và solo giản.
a) phương pháp tính thể tích khối trụ:

Trong đó ta có:
r: nửa đường kính hình trụh: chiều cao hình trụ
b) diện tích xung quanh của khối trụ có công thức như sau:

Trong đó:
r: nửa đường kính hình trụh: độ cao nối từ bỏ đáy cho tới đỉnh của hình trục) cách làm tính diện tích toàn phần


d) Một vài phương pháp hình trụ khác
Diện tích đáy:

Chu vi đáy:

4. Những công thức toán hình lớp 12: khía cạnh cầu
Theo phần đa gì bọn họ đã được học, mặt ước tâm O, nửa đường kính r được khiến cho bởi tập hòa hợp điểm M trong không gian và biện pháp điểm O khoảng cố định và thắt chặt không đổi bằng r (r>0).
Cho mặt mong S (I,R), ta có:
Trong đó: r: nửa đường kính hình mong
Diện tích phương diện cầu:

5. Công thức toán hình 12 tọa độ trong không gian
5.1. Hệ tọa độ oxyz
Trong không khí với hệ tọađộ oxyz, cho tía trục Ox, Oy, Oz vuông góc từng song một và rành mạch nhau, tất cả gốc tọa độ O, trục tung Oy, trục hoành Ox, trục cao Oz và các mặt tọa độ Oxy, Oyz, Ozx. Các


Chú ý:


5.2. Vectơ

5.3. Tích có vị trí hướng của 2 vectơ
Cho 2 vectơ







Tính chất có hướng của 2 vectơ
a.



b.

c.


5.4. Tọa độ điểm

5.5. Phương trình khía cạnh cầu, mặt đường thẳng, phương diện phẳng
a) Phương trình đường thẳng
Các dạng phương trình đường thẳng trong không gian bao gồm:
- Vectơ chỉ phương của mặt đường thẳng:
Định nghĩa: cho đường trực tiếp d. Trường hợp vectơ


Chú ý:
a là VTCP của d thì
Nếu d đi qua hai điểm A, B thì AB là 1 VTCP của d
Trục Ox gồm vecto chỉ phương






- Phương trình thông số của con đường thẳng:
Phương trình tham số của mặt đường thẳng () trải qua điểm


{x=x0+a1t
{y=y0+a2t
z= z0+a3t
- Phương trình thiết yếu tắc của mặt đường thẳng:
Phương trình bao gồm tắc của con đường thẳng (



(


b) Phương trình phương diện cầu
Theo định nghĩa, bạn có thể biết được, phương trình mặt cầu là lúc cho điểm I cố định và thắt chặt và số thực dương R. Call tập hợp hầu như điểm M trong không khí cách I một khoảng tầm R được gọi là mặt ước tâm I, bán kính R.
Lúc này ta gồm hai dạng phương trình:
Dạng 1: Phương trình mặt cầu (S), có tâm I (a,b,c), nửa đường kính R

Dạng 2: Phương trình tất cả dạng:

Với điều kiện là:


c) Phương trình khía cạnh phẳng
- Phương trình khía cạnh phẳng a:
Phương trình tổng quát:


Phương trình đoạn chắn:

( a qua A (a;0;0) ; B ( 0;b;0 ) ; C (0;0;c ))
- Góc giữa 2 khía cạnh phẳng:
a: Ax + By + Cz + D = 0
b: A’x +B’y + C’z + D’ = 0

- khoảng cách từ điểm M0(x0; y0; z0) đến mặt phẳng a:
$d(M,(a))=fracAx_0+By_0+Cz_0+DsqrtA^2+B^x+C^2^$
Đăng ký ngay nhằm được các thầy cô tổng hợp kỹ năng toán 12 và chế tạo lộ trình ôn thi THPT tổ quốc sớm ngay từ bây giờ
Hy vọngcác công thức toán hình 12mà VUIHOC share trên phía trên phần nào giúp các bạn ghi nhớ kết quả và và tinh giảm sai sót trong quy trình làm bài. Nếu mong ước hiểu sâu về bài xích giảng kiến thức Toán 12, các bạn học sinh hãy đk tham gia khóa học dành cho học sinh lớp 12 ôn thi Toán thpt Quốc Gia trên Vuihoc.vn nhé! Chúc chúng ta ôn thi thật hiệu quả.
Nhằm giúp các bạn học sinh lớp 12 rất có thể nhanh giường tra cứu tất cả các cách làm Toán 12, bao hàm công thức Giải tích 12 và cách làm Hình học 12, ship hàng cho quá trình học tập, ôn luyện kiến thức và kỹ năng môn Toán 12, ôn thi THPT giang sơn 2023 môn Toán, toancapba.com chia sẻ đến chúng ta tài liệu bảng tóm tắt phương pháp Toán 12, tài liệu được biên soạn bởi toancapba.com.
KHÓA ÔN CHUYÊN ĐỀ THI TỐT NGHIỆP THPT
NHANH CHÓNG LẤP LỖ HỔNG KIẾN THỨC - TỰ TIN NHẬP CUỘC ĐƯỜNG ĐUA ĐẠI HỌC
✅ hệ thống hóa kỹ năng trọng trung tâm theo từng chăm đề thi xuất sắc nghiệp THPT
✅ cung cấp các phương thức làm bài kết quả theo từng siêng đề
THPT
✅ Lưu ý các lỗi không nên thường chạm mặt và tips, mẹo tăng thêm tốc độ có tác dụng bài
✅ Đầy đủ những môn Toán - Lí - Hóa - Anh - Văn - Sinh - Sử - Địa - GDCD
✅ Học chi phí chỉ 50K/chuyên đề

A. Phương pháp toán 12 đại số
1. Bí quyết lũy vượt 12

2. Cách làm logarit toán 12 đề xuất nhớ

3. Cách làm hàm số lũy thừa – nón – logarit toán 12
Nội dung loài kiến thức:
Công thức hàm số lũy thừaCông thức hàm số mũ
Công thức hàm số logarit
Đồ thị hàm số mũ
Đồ thị hàm số logarit


3. Cách làm phương trình mũ với logarit toán 12
Nội dung con kiến thức:
Công thức Phương trình mũ dạng cơ bảnCông thức Phương trình mũ dạng logarit hóa
Công thức Phương trình logarit dạng cơ bản
Công thức Phương trình logarit dạng nón hóa

4. Công thức bất phương trình mũ cùng logarit toán 12
Nội dung con kiến thức:
Công thức Bất phương trình nón dạng cơ bảnCông thức Bất phương trình logarit dạng cơ bản

5. Phương pháp đạo hàm toán 12 buộc phải nhớ
Nội dung con kiến thức: bí quyết đạo hàm của (sinx, cosx, tanx, cotx)


6. Công thức nguyên hàm toán lớp 12
Tổng vừa lòng bộ công thức nguyên hàm công tác học toán 12 học sinh cần cần nhớ.


7. Công thức diện tích s và thể tích toán 12

8. Công thức vận động toán 12

9. Cách làm lượng giác 12 đề nghị nhớ
Nội dung con kiến thức:
Hệ thức cơ bảnCung liên kết
Công thức cộng
Công thức nhân đôi, nhân ba
Công thức hạ bậc
Công thức chuyển đổi tổng thành tích
Công thức biến đổi tích thành tổng

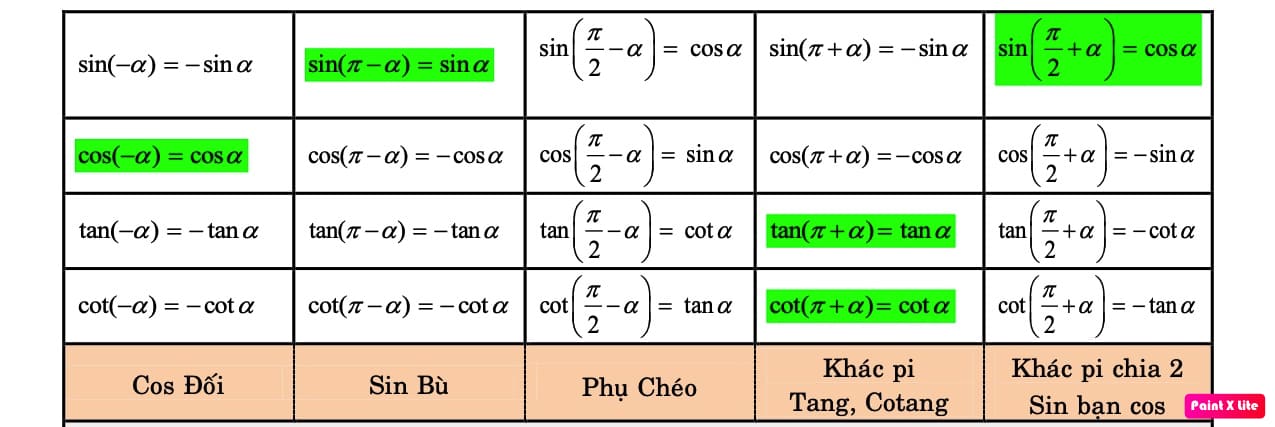




10. Cách làm phương trình lượng giác toán 12


11. Công thức tổ hợp – phần trăm 12 cần nhớ
Nội dung con kiến thức:
Quy tắc cộngQuy tắc nhân
Công thức tính Hoán vị
Công thức tính Chỉnh hợp
Công thức tính Tổ hợp
Công thức tính Xác suất

12. Cách làm khai triển nhị thức newtơn toán 12
Nội dung loài kiến thức:
Công thức khai triển dạng liệt kêCông thức khai triển tổng quát

13. Cách làm Cấp số cộng – cấp cho số Nhân toán 12


14. Khảo sát điều tra hàm số và những dạng toán liên quan
Nội dung loài kiến thức:
Xét tính đối kháng điệu hàm sốHàm số bậc 3Hàm tốt nhất biến
Điều kiện rất trị
Cực trị hàm số bậc 3Cực trị của hàm số bậc 4Tìm max – min trên đoạn
Tìm max – min trên khoảng
Tiệm cận đứng
Tiệm cận ngang
Tìm tọa độ giao điểm hoặc số giao điểm hai đồ gia dụng thị
Phương trình tiếp tuyến



15. Số phức và các yếu tố liên quan

B. Công thức toán hình 12
1. Khối nhiều diện với thể tích của chúng
Nội dung kiến thức:
Mộ số hình phẳng cơ bảnTam giác vuông
Tam giác đều
Tam giác thường
Hình vuông
Hình chữ nhật
Hình thoi
Thể tích khối chóp
Hình chóp
Hình chóp tam giác đều
Hình chóp tứ diện đều
Hình chóp tứ giác đều
Hình chóp có lân cận SA vuông góc với mặt phẳng đáy
Hình chóp xuất hiện bên (SAB) vuông góc với mặt phẳng đáy
Thế tích khối lăng trụ
Hình lăng trụ thường
Hình lăng trụ đứng
Hình hộp




2. Phương diện trụ – khía cạnh nón – mặt cầu
Nội dung con kiến thức:
Công thức toán hình 12 khía cạnh nónCông thức toán hình 12 phương diện trụ
Công thức toán hình 12 khía cạnh cầu
Cách tìm bán kính mặt ước ngoại tiếp hình chóp thường gặp
Hình chóp có những đỉnh chú ý một cạnh bên dưới một góc vuông Hình chóp đều
Hình chóp có ở kề bên vuông góc với khía cạnh phẳng đáy
Hình chóp có mặt bên vuông góc với khía cạnh đáy
3. Hình học tập giải tích trong không gian
Nội dung loài kiến thức:
Công thức toán hình 12 Hệ trục tọa độ OxyzCông thức toán hình 12 Tọa độ vectơ
Công thức toán hình 12 Tọa độ điểm
Công thức toán hình 12 Tích có hướng của hai vectơ
Công thức toán hình 12 Phương trình mặt cầu
Công thức toán hình 12 Phương trình khía cạnh phẳng
Công thức toán hình 12 Vị trí kha khá giữa khía cạnh phẳng với mặt cầu
Phương trình đường thẳng
Công thức toán hình 12 Vị trí kha khá giữa hai tuyến phố thẳng
Công thức toán hình 12 Vị trí tương đối giữa mặt đường thẳng và mặt phẳng
Công thức toán hình 12 khoảng cách từ điểm đến chọn lựa đường thẳng
Công thức toán hình 12 Góc giữa hai đường thẳng
Công thức toán hình 12 Góc giữa đường thẳng với mặt phẳng
Hình chiếu và điểm đối xứng
Trên đấy là Full công thức Toán 12 cơ bạn dạng – cải thiện | hình học, đại số học viên cần đề nghị nhớ.








