Kì thi tuyển chọn sinh vào lớp 10 sắp tới đây gần. Các em học sinh đang mắc ôn tập để chuẩn bị cho mình kiến thức thật vững rubi để từ bỏ tin phi vào phòng thi. Vào đó, toán là 1 môn thi cần và khiến nhiều người học sinh lớp 9 cảm giác khó khăn. Để giúp các em ôn tập môn Toán hiệu quả, công ty chúng tôi xin ra mắt tài liệu tổng đúng theo các vấn đề hình ôn thi vào lớp 10.
Như các em vẫn biết, so với môn Toán thì những bài toán hình được nhiều bạn đánh giá là rất khó hơn không hề ít so cùng với đại số. Trong số đề thi toán lên lớp 10, câu hỏi hình chiếm một số trong những điểm khủng và yêu cầu các em ý muốn được số điểm khá xuất sắc thì buộc phải làm được câu toán hình. Để giúp các em rèn luyện phương pháp giải các bài toán hình 9 lên 10, tài liệu shop chúng tôi giới thiệu là những bài toán hình được chọn lọc trong các đề thi các thời gian trước trên cả nước. Ở mỗi bài xích toán, cửa hàng chúng tôi đều hướng dẫn phương pháp vẽ hình, chỉ dẫn lời giải chi tiết và kèm theo lời bình sau mỗi việc để lưu ý lại các điểm chủ quản của bài xích toán. Hy vọng, phía trên sẽ là 1 trong những tài liệu có ích giúp những em rất có thể làm tốt bài toán hình vào đề với đạt điểm cao trong kì thi sắp tới.
Bạn đang xem: Một số bài toán hình lớp 9 thi vào 10
I.Các việc hình ôn thi vào lớp 10 chọn lọc không cất tiếp tuyến.
Bài 1: mang lại nửa đường tròn (O) 2 lần bán kính AB= 2R, dây cung AC. điện thoại tư vấn M là điểm ở trung tâm cung AC. Một mặt đường thẳng kẻ từ điểm C tuy nhiên song cùng với BM và cắt AM nghỉ ngơi K , giảm OM ngơi nghỉ D. OD giảm AC trên H.
1. Chứng tỏ CKMH là tứ giác nội tiếp.
2. CMR : CD = MB ; DM = CB.
3. Xác điểm C trên nửa đường tròn (O) để AD chính là tiếp đường của nửa mặt đường tròn.
Bài giải chi tiết:
1. CMR tứ giác CKMH là tứ giác nội tiếp.AMB = 90o (vì là góc nội tiếp chắn nửa mặt đường tròn). => AM ⊥ MB. Nhưng mà CD // BM (theo đề) buộc phải CD ⊥ AM . Vậy MKC = 90o.
Cung AM = cung cm (gt) => OM ⊥ AC => MHC = 90o.
Tứ giác CKMH tất cả MKC + MHC = 180o buộc phải nội tiếp đượctrong một đường tròn.
2. CMR: CD = MB ; DM = CB.Ta có: ngân hàng á châu = 90o (vì là góc nội tiếp chắn nửa con đường tròn)
Suy ra DM // CB . Lại có CD // MB nên CDMB là một trong những hình bình hành. Từ kia ta suy ra: CD = MB và DM = CB.
3. Ta có: AD là một trong những tiếp con đường của đường tròn (O) ⇔ AD ⊥ AB. ΔADC bao gồm AK vuông góc với CD cùng DH vuông góc với AC bắt buộc điểm M là trực trọng điểm tam giác . Suy ra: centimet ⊥ AD.Vậy AD ⊥ AB ⇔ cm // AB ⇔ cung AM = cung BC.
Mà AM = MC yêu cầu cung AM = cung BC ⇔ AM = cung MC = cung BC = 60o.
Lời bình:
1. Rõ ràng câu 1, hình vẽ nhắc nhở cho ta cách minh chứng các góc H và K là đa số góc vuông, và để có được góc K vuông ta chỉ cần chỉ ra MB vuông góc với AM cùng CD tuy vậy song với MB. Điều này được tìm ra trường đoản cú hệ quả góc nội tiếp và giả thiết CD tuy vậy song với MB. Góc H vuông được suy từ kết quả của bài số 14 trang 72 SGK toán 9 tập 2. Những em lưu ý các bài bác tập này được áp dụng vào việc giải các câu hỏi hình ôn thi vào lớp 10 khác nhé.2. Không cần thiết phải bàn, kết luận gợi ngay thức thì cách chứng minh phải không các em?3. Cụ thể đây là thắc mắc khó so với một số em, bao gồm cả khi phát âm rồi vẫn lừng chừng giải ra sao , có tương đối nhiều em may mắn hơn vẽ ngẫu nhiên là rơi trúng vào hình 3 sống trên từ kia nghĩ ngay được vị trí điểm C bên trên nửa con đường tròn. Khi gặp loại toán này đòi hỏi phải tứ duy cao hơn. Thông thường nghĩ ví như có kết quả của việc thì sẽ xảy ra điều gì ? Kết hợp với các đưa thiết và các hiệu quả từ các câu bên trên ta tìm kiếm được lời giải của bài bác toán.Bài 2: Cho ABC tất cả 3 góc nhọn. Đường tròn có đường kính BC cắt hai cạnh AB, AC thứu tự tại các điểm E cùng F ; BF cắt EC trên H. Tia AH BC trên điểm N.
a) CMR: tứ giác HFCN là tứ giác nội tiếp.b) CMR: FB là tia phân giác của góc EFN.c) trường hợp AH = BC. Hãy search số đo góc BAC trong ΔABC.

Bài giải đưa ra tiết:
a) Ta có: BFC = BEC = 90o
(vì là góc nội tiếp chắn nửa mặt đường tròn 2 lần bán kính BC)
Tứ giác HFCN có HFC = HNC = 180o cho nên nó nội tiếp được trongđường tròn 2 lần bán kính HC) (đpcm).
b) Ta bao gồm EFB = ECB (hai góc nội tiếp cùng chắn cung BE của mặt đường tròn 2 lần bán kính BC).
ECB = BFN (hai góc nội tiếp cùng chắn cung hà nội của con đường tròn 2 lần bán kính HC).
Suy ra: EFB = BFN. Từ đó suy ra FB là tia phân giác của góc EFN.
c) Xét ΔFAH với ΔFBC: AFH = BFC = 90o, AH bằng đoạn BC (gt), FAH = FBC (cùng phụ với góc ACB). Vì đó: ΔFAH = ΔFBC (cạnh huyền- góc nhọn). Từ đó suy ra: FA = FB.
ΔAFB là tam giác vuông trên F; FA = FB cho nên nó vuông cân. Do đó BAC = 45o
II. Các bài toán hình ôn thi vào lớp 10 bao gồm chứa tiếp tuyến.
Bài 3: Cho nửa con đường tròn chổ chính giữa O cùng nó có đường kính AB. Xuất phát điểm từ một điểm M nằm ở tiếp tuyến Ax của nửa con đường tròn, ta vẽ tiếp con đường thứ hai tên thường gọi là MC (trong kia C là tiếp điểm). Từ C hạ CH vuông góc cùng với AB, MB giảm (O) tại điểm Q và giảm CH trên điểm N. Call g I = MO ∩ AC. CMR:
a) Tứ giác AMQI là tứ giác nội tiếp.b) Góc AQI = góc ACOc) công nhân = NH.(Trích đề thi tuyển sinh vào lớp 10 năm học 2009-2010 của sở GD&ĐT thức giấc Bắc Ninh)

Bài giải bỏ ra tiết:
a) Ta có: MA = MC (tính hóa học hai tếp tuyến giảm nhau), OA = OC (bán kính con đường tròn (O))Do đó: MO ⊥ AC => MIA = 90o.
AQB = 90o (vì là góc nội tiếp chắn nửa đường tròn )
=> MQA = 90o. Nhì đỉnh I và Q cùng nhìn AM bên dưới một góc vuông đề xuất tứ giác AMQI nội tiếp được trong một đường tròn.
b) Tứ giác AMQI nội tiếp đề nghị AQI = AMI (cùng phụ góc MAC) (2).
ΔAOC gồm OA bằng với OC nên nó cân trên O. => CAO = ACO (3). Trường đoản cú (1), (2) (3) ta suy ra AQI = ACO.
c) chứng tỏ CN = NH.Gọi K = BC∩ Ax. Ta có: acb = 90o (vì là góc nội tiếp chắn nửa đường tròn).
AC vuông góc với BK , AC vuông góc cùng với OM OM tuy nhiên song với BK. Tam giác ABK có: OA = OB cùng OM // BK bắt buộc ta suy ra MA = MK.
Theo hệ trái ĐLTa let cho gồm NH tuy nhiên song AM (cùng vuông góc AB) ta được:



Lời bình
1. Câu một là dạng toán chứng minh tứ giác nội tiếp thường chạm chán trong các vấn đề hình ôn thi vào lớp 10. Mẫu vẽ gợi đến ta suy nghĩ: Cần chứng minh hai đỉnh Q và I cùng quan sát AM dưới một góc vuông. Góc AQM vuông bao gồm ngay vì kề bù với acb vuông, góc MIA vuông được suy từ tính chất hai tiếp tuyến giảm nhau.2. Câu 2 được suy từ bỏ câu 1, thuận tiện thấy tức thì AQI = AMI, ACO = CAO, sự việc lại là đề nghị chỉ ra IMA = CAO, vấn đề này không khó phải không các em?3. Vì CH // MA , cơ mà đề toán yêu thương cầu minh chứng CN = NH ta nghĩ ngay lập tức việc kéo dài đoạn BC đến khi cắt Ax tại K . Khi ấy bài toán vẫn thành dạng thân quen thuộc: cho tam giác ABC cùng M là trung điểm của BC. Vẽ con đường thẳng d tuy vậy song BC giảm AB, AC ,AM theo thứ tự tại E, D, I. CMR : IE = ID. Ghi nhớ được những bài toán có liên quan đến một trong những phần của bài thi ta qui về vấn đề đó thì giải quyết đề thi một bí quyết dễ dàng.Bài 4: Cho con đường tròn (O) có đường kính là AB. Trên AB rước một điểm D nằm kế bên đoạn trực tiếp AB với kẻ DC là tiếp con đường của mặt đường tròn (O) (với C là tiếp điểm). điện thoại tư vấn E là hình chiếu hạ trường đoản cú A ra đường thẳng CD và F là hình chiếu hạ trường đoản cú D xuống AC.
Chứng minh:
a) Tứ giác EFDA là tứ giác nội tiếp.b) AF là tia phân giác của góc EAD.c) Tam giác EFA và BDC là nhì tam giác đồng dạng.d) nhị tam giác ACD và ABF gồm cùng diện tích với nhau.(Trích đề thi xuất sắc nghiệp và xét tuyển chọn vào lớp 10- năm học 2000- 2001)

Bài giải bỏ ra tiết:
a) Ta có: AED = AFD = 90o (gt). Hai đỉnh E và F cùng nhìn AD bên dưới góc 90o đề nghị tứ giác EFDA nội tiếp được trong một mặt đường tròn.
b)Ta có:

Tam giác AOC cân nặng tại O ( OA = OC = nửa đường kính R) đề nghị suy ra CAO = OCA. Do đó: EAC = CAD. Vì thế AF là tia phân giác của góc EAD (đpcm).
ΔEFA cùng ΔBDC có:
EFA = CDB (hai góc nội tiếp thuộc chắn cung của con đường tròn nước ngoài tiếp tứ giác EFDA).


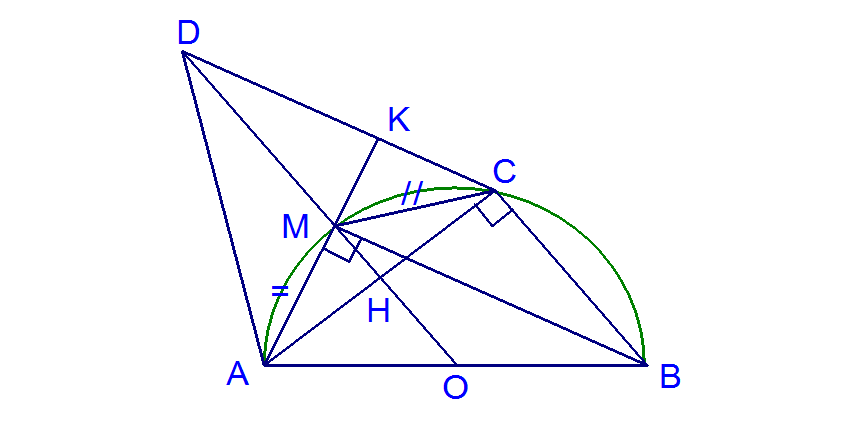
Bài 5: Cho tam giác ABC (BAC o) là tam giác nội tiếp trong nửa con đường tròn trọng điểm O có 2 lần bán kính AB. Vẽ tiếp con đường của mặt đường tròn (O) trên C và hotline H là hình chiếu kẻ từ A đến tiếp con đường . Đường trực tiếp AH cắt đường tròn (O) tại M (M ≠ A). Đường thẳng kẻ từ M vuông góc với AC giảm AC trên K với AB trên P.
a) CMR tứ giác MKCH là 1 tứ giác nội tiếp.b) CMR: map là tam giác cân.c) Hãy chỉ ra điều kiện của ΔABC để M, K, O cùng nằm trên một đường thẳng.
Bài giải bỏ ra tiết:
a) Ta tất cả : MHC = 90o(gt), MHC = 90o (gt)Tứ giác MKCH tất cả tổng nhị góc đối nhau bởi 180o nên tứ giác MKCH nội tiếp được trong một đường tròn.
b) AH song song với OC (cùng vuông góc CH) yêu cầu MAC = ACO (so le trong)ΔAOC cân ở O (vì OA = OC = bán kính R) cần ACO = CAO. Vì đó: MAC = CAO. Vậy AC là phân giác của MAB. Tam giác maps có đường cao AK (vì AC vuông góc MP), cùng AK cũng là con đường phân giác suy ra tam giác maps cân sống A (đpcm).
Xem thêm: Tổng Hợp Đề Thi Giữa Kì 1 Môn Toán 11 2.1, Toán Học Lớp 11
Ta tất cả M; K; p thẳng hàng phải M; K; O thẳng sản phẩm nếu phường trùng với O tuyệt AP = PM. Theo câu b tam giác maps cân ngơi nghỉ A yêu cầu ta suy ra tam giác maps đều.Do kia CAB = 30o. Ngược lại: CAB = 30o ta chứng tỏ P=O:
Khi CAB = 30o => MAB = 30o (vì tia AC là phân giác của MAB) . Vị tam giác MAO cân tại O lại sở hữu MAO = 60o đề xuất MAO là tam giác đều. Vì đó: AO = AM. Cơ mà AM = AP (do ΔMAP cân nặng ở A) đề nghị suy ra AO = AP. Vậy P=O.
Trả lời: Tam giác ABC mang lại trước tất cả CAB = 30o thì tía điểm M; K ;O cùn vị trí một mặt đường thẳng.
Bài 6: mang lại đường tròn tâm O có đường kính là đoạn trực tiếp AB có bán kính R, Ax là tiếp con đường của mặt đường tròn. Trên Ax vẽ một điểm F làm thế nào để cho BF cắt (O) trên C, mặt đường phân giác của góc ABF giảm Ax tại điểm E và giảm đường tròn (O) trên điểm D.
a) CMR: OD tuy vậy song BC.b) centimet hệ thức: BD.BE = BC.BFc) CMR tứ giác CDEF là tứ giác nội tiếp.

Bài giải bỏ ra tiết:
a) ΔBOD cân nặng tại O (do OD = OB = nửa đường kính R) => OBD = ODB
Mà OBD = CBD (gt) yêu cầu ODB = CBD. Bởi đó: OD // BC.
ADB = 90o (vì là góc nội tiếp chắn nửa mặt đường tròn (O) => AD ⊥ BE.ACB = 90o (vì là góc nội tiếp chắn nửa đường tròn (O) => AC ⊥ BF.
ΔEAB vuông trên A (do Ax là mặt đường tiếp đường ), tất cả AD vuông góc BE nên:
AB2 = BD.BE (1).
ΔEAB vuông tại A (do Ax là con đường tiếp tuyến), bao gồm AC vuông góc BF nên
AB2 = BC.BF (2).
Theo (1) cùng (2) ta suy ra: BD.BE = BC.BF.
c) Ta có:
CDB=CAB (vì là 2 góc nội tiếp thuộc chắn cung BC)
CAB=CFA ( vì là 2 góc cùng phụ cùng với góc FAC)
Do kia : góc CBD=CFA.
Do kia tứ giác CDEF nội tiếp.
Cách khác
ΔDBC và có ΔFBE: góc B tầm thường và

Lời bình
1. Với câu 1, tự gt BD là phân giác góc ABC kết hợp với tam giác cân nặng ta nghĩ ngay đến cần chứng tỏ hai góc so le trong ODB và OBD bằng nhau.2. Việc chăm chú đến những góc nội tiếp chắn nửa mặt đường tròn kết phù hợp với tam giác AEB, FAB vuông vì Ax là tiếp tuyến lưu ý ngay đến hệ thức lượng vào tam giác vuông quen thuộc. Mặc dù vẫn tất cả thể minh chứng hai tam giác BDC với BFE đồng dạng trước rồi suy ra BD.BE = BC.BF. Với phương pháp thực hiện này còn có ưu câu hỏi hơn là giải luôn luôn được câu 3. Các em thử triển khai xem sao?3. Trong toàn bộ các câu hỏi hình ôn thi vào lớp 10 thì chứng tỏ tứ dạng nội tiếp là dạng toán cơ bạn dạng nhất. Khi giải được câu 2 thì câu 3 rất có thể sử dụng câu 2 , hoặc có thể chứng tỏ theo giải pháp 2 như bài bác giải.
Bài 7: từ bỏ điểm A ở đi ngoài đường tròn (O), kẻ nhị tiếp tuyến AB, AC tới đường tròn ( B, C là những tiếp điểm). Đường thẳng trải qua A cắt đường tròn (O) tại nhì điểm D với E (trong đó D nằm giữa A và E , dây DE không qua trọng điểm O). Rước H là trung điểm của DE cùng AE cắt BC trên điểm K .
a) CMR: tứ giác ABOC là 1 tứ giác nội tiếp.b) CMR: HA phân giác của góc BHCc) CMR: :

Bài giải chi tiết:
a) ABO = ACO = 90o (tính chất tiếp tuyến)Tứ giác ABOC tất cả ABO + ACO = 180o nên là 1 trong những tứ giác nội tiếp.
b) AB = AC (theo đặc thù tiếp tuyến giảm nhau). Suy ra: cung AB = AC. Vì thế AHB = AHC. Vậy HA là phân giác của góc BHC.c) chứng minh :
ΔABD với ΔAEB có:
Góc BAE chung, ABD = AEB (cùng bằng 50% sđ cung BD)
Suy ra : ΔABD ~ ΔAEB

Bài 8: mang đến nửa mặt đường tròn (O) có 2 lần bán kính AB = a. Gọi hai tia Ax, By là những tia vuông góc cùng với AB ( Ax, By thuộc cùng một nửa khía cạnh phẳng bờ AB). Sang 1 điểm M thuộc nửa đường tròn (O) (M không trùng cùng với A với B), vẻ những tiếp đường với nửa mặt đường tròn (O); chúng cắt Ax, By theo thứ tự tại 2 điểm E cùng F.
1. Hội chứng minh: EOF = 90o
2. Minh chứng tứ giác AEMO là 1 tứ giác nội tiếp; nhị tam giác MAB với OEF đồng dạng.
3. Gọi K là giao của hai tuyến phố AF cùng BE, chứng tỏ rằng MK ⊥ AB.
4. Trường hợp MB = √3.MA, tính S tam giác KAB theo a.

Bài giải bỏ ra tiết:
1. EA, EM là nhì tiếp đường của con đường tròn (O)cắt nhau nghỉ ngơi E bắt buộc OE là phân giác của AOM.
Tương tự: OF là phân giác của góc BOM.
Mà AOM cùng BOM là 2 góc kề bù nên: EOF = 90o (đpcm)
2. Ta có: EAO = EMO = 90o (tính hóa học tiếp tuyến)Tứ giác AEMO gồm EAO + EMO = 180o cần nội tiếp được vào một mặt đường tròn.
Hai tam giác AMB cùng EOF có: AMB = EOF = 90o cùng MAB = MEO (vì 2 góc thuộc chắn cung MO của mặt đường tròn ngoại tiếp tứ giác AEMO. Từ đó suy ra: tam giác AMB và EOF là 2 tam giác đồng dạng với nhau (g.g).
3. Tam giác AEK bao gồm AE tuy nhiên song với FB nên:



Lời bình
(Đây là đề thi tuyển chọn sinh vào lớp 10 năm học tập 2009-2010 của tỉnh Hà Nam) .
Trong các việc ôn thi vào lớp 10, tự câu a cho câu b chắc hẳn rằng thầy cô nào đã từng có lần cũng ôn tập, cho nên những em làm sao ôn thi nghiêm túc chắc chắn giải được ngay, khỏi nên bàn. Bài toán 4 này còn có 2 câu nặng nề là c và d, và đó là câu khó mà bạn ra đề khai thác từ câu: MK cắt AB làm việc N. Chứng minh: K là trung điểm MN.
Nếu ta quan ngay cạnh kĩ MK là con đường thẳng chứa đường cao của tam giác AMB ngơi nghỉ câu 3 và 2 tam giác AKB với AMB có chung đáy AB thì ta đang nghĩ ngay đến định lí: nếu hai tam giác gồm chung đáy thì tỉ số diện tích s hai tam giác bằng tỉ số hai đường cao tương ứng, bài toán qui về tính diện tích s tam giác AMB chưa hẳn là khó yêu cầu không các em?
bên trên đây, chúng tôi vừa giới thiệu chấm dứt các việc hình ôn thi vào lớp 10 tất cả đáp án chi tiết. Giữ ý, để mang được điểm trung bình những em cần phải làm kĩ dạng toán chứng tỏ tứ giác nội tiếp vì đó là dạng toán chắc chắn rằng sẽ chạm mặt trong hồ hết đề thi tuyển sinh lớp 10 môn Toán. Các câu còn lại sẽ là những bài xích tập tương quan đến các đặc thù khác về cạnh với góc vào hình hoặc tương quan đến tiếp tuyến của con đường tròn. Một yêu mong nữa là các em cần phải rèn luyện năng lực vẽ hình, nhất là vẽ mặt đường tròn bởi vì trong cấu tạo đề thi nếu như hình vẽ không đúng thì bài xích làm sẽ không được điểm. Các bài tập trên đây công ty chúng tôi chọn lọc gần như chứa hầu hết dạng toán thường chạm mặt trong các đề thi toàn quốc nên cực kì thích thích hợp để các em tự ôn tập trong năm này. Hy vọng, cùng với những việc hình này, những em học viên lớp 9 vẫn ôn tập thật xuất sắc để đạt tác dụng cao vào kì thi vào 10 sắp tới.
Mua tài khoản tải về Pro để đề xuất website toancapba.com KHÔNG quảng cáo & tải File rất nhanh chỉ từ 79.000đ. Mày mò thêm100 câu hỏi Hình học tập lớp 9 có giải mã được soạn theo chuẩn kiến thức, kĩ năng chương trình sách giáo khoa lớp 9. Đây toàn là những bài toán nổi bật thường xuất hiện thêm trong các bài thi vào lớp 10.
Lưu ý: 100 bài tập bao gồm đáp án giải đưa ra tiết chúng ta tải file về để thấy nhé.
100 câu hỏi Hình học lớp 9 gồm lời giải
Bài 1:
Cho DABC có những đường cao BD cùng CE. Đường thẳng DE cắt đường tròn ngoại tiếp tam giác tại nhì điểm M và N.
1. Triệu chứng minh: BEDC nội tiếp.
2. Hội chứng minh:

3. Chứng minh: DE song song với tiếp tuyến đường tai A của con đường tròn ngoại tiếp tam giác.
4. điện thoại tư vấn O là chổ chính giữa đường tròn nước ngoài tiếp tam giác ABC. Hội chứng minh: OA là phân giác của góc

5. Hội chứng tỏ: AM2=AE. AB.
Bài 2:
Cho(O) đường kính AC. Trên đoạn OC lấy điểm B với vẽ con đường tròn trọng điểm O’, 2 lần bán kính BC. Gọi M là trung điểm của đoạn AB. Tự M vẽ dây cung DE vuông góc với AB;DC cắt đường tròn trung khu O’ tại I.
1. Tứ giác ADBE là hình gì?
2. C/m DMBI nội tiếp.
3. C/m B;I;E thẳng hàng với MI=MD.
4. C/m MC. DB=MI. DC
5. C/m mi là tiếp tuyến đường của (O’)
Bài 3:
Cho DABC gồm

3. C/m CA là phân giác của góc BCS.
Bài 4:
Cho DABC tất cả

1. C/m ADCB nội tiếp.
2. C/m ME là phân giác của góc AED.
3. C/m:

4. Chứng tỏ ME là phân giác của góc AED.
5. C/m ba đường thẳng BA;EM;CD đồng quy.
Bài 5:
Cho tam giác ABC có 3 góc nhọn cùng AB chia sẻ bởi: Trịnh Thị Thanh
Liên kết mua về








