



Chia sẻ:




Tuyển chọn 400 bài xích Tập Toán Lớp 11 - Hình Học
Nội dung của cuốn sách Tuyển lựa chọn 400 bài Tập Toán Lớp 11 (Hình Học) được chia thành 3 chương chính, rõ ràng như sau:
Chương I: Phép dời hình với phép đồng dạng trong mặt phẳng
Chương II: Đường thẳng với mặt phẳng trong không gian quan hệ tuy vậy song
Chương III: Vectơ trong không gian, quan hệ vuông góc.
Bạn đang xem: Bài tập toán hình lớp 11
Cuốn sách nói đến phần nhiều các vấn đề cơ phiên bản của chương trình Toán lớp 11, giúp những em học tập sinh có tài năng liệu từ ôn tập và khối hệ thống hóa những kiến thức cơ bản, nâng cao để chuẩn bị tốt cho các kì thi quan lại trọng.
Cuốn sách sẽ là 1 trong những tài liệu góp ích cho các em trong quy trình tự học, giúp những em tự tập luyện để nâng cao năng lực giải toán của mình.
THÔNG TIN & KHUYẾN MÃI
Có thể chúng ta quan tâm

Các Dạng Toán Điển Hình Giải Tích 11 Tập 2
Giá bán: 37.410 đ 43.500 đ

Học giỏi Đại Số cùng Giải Tích 11
Giá bán: 73.500 đ 98.000 đ

Phân Dạng Và phương pháp Giải Toán Đại Số & Giải Tích Lớp 11 Cơ Bản
Giá bán: 49.560 đ 59.000 đ

Hướng Dẫn Học cùng Giải cụ thể Bài Tập Toán 11
Giá bán: 58.500 đ 78.000 đ
Về Chu Văn Biên
chế độ
Chương mặt đường thẳng cùng mặt phẳng trong không gian, quan tiền hệ tuy vậy song là chương quan liêu trọng bắt đầu về hình học không khí trong lịch trình toán hình học tập lớp 11. Trong số ấy bài đại cương về con đường thẳng cùng mặt phẳng là giữa những bài đặc biệt quan trọng nhất để các em có thể học xuất sắc những kiến thức sau này. Vày vậy, công ty chúng tôi đã tổng hợp định hướng và sẽ hướng dẫn những em giải một số bài bác tập toán hình 11 về đại cương về đường thẳng cùng mặt phẳng bám sát chương trình sách giáo khoa. Hy vọng tài liệu này sẽ mang đến nhiều hữu ích cho các em.

I. Các kiến thức phải nắm nhằm giải bài bác tập toán hình 11: Đại cương cứng về mặt đường thẳng và mặt phẳng
Để giải được những bài tập toán hình 11 phần đại cương cứng về mặt đường thẳng và mặt phẳng thì những em bắt buộc nắm rõ những kiến thức sau đây:
1. Các tiên đề về hình học tập không gian
Tiên đề 1: gồm một và có một mặt phẳng trải qua ba điểm ko thẳng sản phẩm đã mang đến trước

Tiên đề 2: Có ít nhất bốn điểm trong không khí sẽ không nằm bên trên một mặt phẳng
Tiên đề 3: Nếu tất cả một đường thẳng cùng một khía cạnh phẳng tất cả hai điểm tầm thường thì mặt đường thẳng này nằm toàn diện trong mặt phẳng trên.
Tiên đề 4: Nếu bao gồm hai phương diện phẳng bao gồm điểm chung thì chúng gồm vô số điểm phổ biến khác nữa (tất cả các điểm tầm thường này tạo nên thành con đường thẳng điện thoại tư vấn là giao tuyến đường của nhì mặt phẳng).
Tiên đề 5: bên trên một phương diện phẳng tùy ý trong không gian các định lý về hình học tập sơ cấp đầy đủ đúng.
Tiên đề 6: từng đoạn thẳng trong một ko gian đều có độ dài đúng chuẩn ( bảo toàn về độ dài, số đo góc và các tính chất liên quan vẫn biết trong hình học phẳng).
2. Cách xác định một mặt phẳng
Có 4 cách xác minh một mặt phẳng:
Cách 1: gồm duy độc nhất vô nhị một khía cạnh phẳng đi qua ba điểm ko thẳng hàng mang lại trước
Cách 2: Có độc nhất vô nhị một mặt phẳng trải qua đường thẳng và một điểm nằm ở ngoài đường thẳng đó.
Cách 3: gồm duy tốt nhất một và có một mặt phẳng trải qua hai con đường thẳng cắt nhau.
Cách 4: có duy độc nhất một khía cạnh phẳng trải qua hai đường thẳng tuy vậy song nhau.
Lưu ý: Cách khẳng định 2 đường thẳng a và b chéo nhau (tức là a, b không đồng phẳng).

- xác định mp(): b ⊂ ()
- lúc đó, ta có: a ∩ () = A
- Nếu: A ∉ b thì a, b chéo cánh nhau
3. Hình chóp cùng hình tứ diện đều
Định nghĩa: trong một mặt phẳng (P) mang đến đa giác, điểm S ∉ (P). Nối S với những đỉnh của nhiều giác. Hình được tạo bởi miền nhiều giác và các miền tam giác trên hotline là hình chóp. ( S: đỉnh, miền nhiều giác: đáy, những miền tam giác: những mặt bên)

- cam kết hiệu: S.ABCD
S: đỉnh
ABCD: phương diện đáy
SA, SB, SC, SD: các cạnh bên
AB, BC, CD, DA: các cạnh đáy
(SAB), (SBC), (SCD), (SDA): các mặt bên
- Tứ diện: Hình chóp bao gồm đáy là 1 trong những tam giác được điện thoại tư vấn là tứ diện
- Tứ diện đều: hình chóp gồm 4 phương diện là những tam giác đều.
II. Gợi ý giải bài xích tập toán hình 11: Đại cương về mặt đường thẳng và mặt phẳng
Chúng tôi đã trích những bài tập toán hình 11 về đại cưng cửng về đường thẳng và mặt phẳng từ bỏ SGK hình học 11 dưới đây:

Bài 1/ SGK hình học tập 11 trang 53
Đề bài: Cho điểm A không phía trong mặt phẳng (α) chứa tam giác BCD. Lấy E với F là những điểm thứu tự nằm trên những cạnh AB với AC.
a) chứng minh rằng con đường thẳng EF bên trong mặt phẳng (ABC).
b) đưa sử EF với BC giảm nhau tại I, chứng minh I là điểm chung của nhị mặt phẳng (BCD) cùng (DEF).
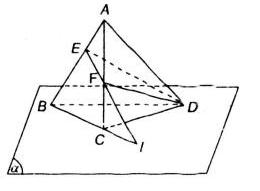
Hướng dẫn giải:
a) Ta có: E ∈ AB nhưng AB ⊂ (ABC)
⇒ E ∈ (ABC)
⇒ F ∈ AC nhưng AC ⊂ (ABC)
⇒ F ∈ (ABC)
b) Đường trực tiếp EF gồm hai điểm E, F thuộc thuộc mp(ABC) bắt buộc theo định đề 3 thì EF ⊂ (ABC).
Ta có: I ∈ BC cơ mà BC ⊂ (BCD) bắt buộc I ∈ (BCD) (1)
I ∈ EF nhưng mà EF ⊂ (DEF) ⇒ I ∈ (DEF) (2)
Từ (1) và (2) ⇒ I là điểm chung của nhì mặt phẳng (BCD) và (DEF).
Bài 2/ SGK hình học tập trang 53
Đề bài: gọi M là giao điểm của mặt đường thẳng d cùng mặt phẳng (α). Minh chứng rằng M là vấn đề chung của (α) với ngẫu nhiên mặt phẳng nào đựng đường thẳng d.

Hướng dẫn giải:
Giả sử bao gồm một phương diện phẳng (β) ngẫu nhiên chứa con đường thẳng d.
Ta có: M là vấn đề chung của d cùng (α) nên: M ∈ (α) (1)
Ta lại có: M ∈ d, nhưng mà d ⊂ (β) ⇒ M ∈ (β) (2).
Từ (1) với (2) ⇒M là điểm chung của hai mặt phẳng (α) cùng (β).
Bài 3/ SGK hình học trang 53
Đề bài: Cho cha đường trực tiếp d1, d2, d3 không phía trong một phương diện phẳng và giảm nhau từng song một. Chứng tỏ ba mặt đường thẳng bên trên đồng quy.
Xem thêm: Giải Bài 4 Trang 17 Sgk Toán 10 Chân Trời Sáng Tạo Tập 2 Trang 17
Hướng dẫn giải:
Gọi I = d1 ∩ d2 cùng (P) là phương diện phẳng chứa (d1) và (d2).
Gọi d3 ∩ d1 = M; d3 ∩ d2 = N. Ta có:
+ M ∈ d1, cơ mà d1 ⊂ (P) ⇒ M ∈ (P)
+ N ∈ d2, nhưng d2 ⊂ (P) ⇒ N ∈ (P).
Nếu M ≠ N ⇒ d3 gồm hai điểm M, N thuộc thuộc (P)
⇒ d3 ⊂ (P)
⇒ d1; d2; d3 đồng phẳng (trái với trả thiết).
⇒ M ≡ N
⇒ M ≡ N ≡ I
Vậy tía đường thẳng d1; d2; d3 đồng quy.
Bài 4/ SGK hình học tập trang 53
Đề bài: Cho tứ điểm A, B, C với D ko đồng phẳng. Hotline GA, GB, GC, GD thứu tự là trọng tâm của các tam giác sau: BCD, CDA, ADB, ACB. Chứng tỏ rằng AGA, BGB, CGC, DGD đồng quy.
Hướng dẫn giải:

Gọi N là trung điểm CD.
+ GA là trung tâm ΔBCD
⇒ GA ∈ trung con đường BN ⊂ (ANB)
⇒ AGA ⊂ (ANB)
GB là trung tâm ΔACD
⇒ GB ∈ trung con đường AN ⊂ (ANB)
⇒ BGB ⊂ (ANB).
Trong mp(ANB): AGA không tuy vậy song với BGB
⇒ AGA giảm BGB tại O
+ minh chứng tương tự: BGB cắt CGC; CGC giảm AGA.
+ CGC không phía bên trong (ANB) ⇒ AGA; BGB; CGC không đồng phẳng(áp dụng tác dụng của bài xích 3).
⇒ AGA; BGB; CGC đồng quy tại O
+ chứng tỏ tương tự cho: AGA; BGB; DGD đồng quy trên O.
Vậy AGA; BGB ; CGC; DGD đồng quy trên O.
Bài 5/ SGK hình học trang 53
Đề bài: Tứ giác ABCD bên trong mặt phẳng (α) gồm hai cạnh AB với CD không tuy vậy song với nhau. Call S là điểm nằm mẫu mã phẳng (α) và M là trung điểm của đoạn SC.
a) search giao điểm N của mặt đường thẳng SD cùng mp (MAB).
b) hotline O là giao điểm của AC cùng BD. Minh chứng rằng cha đường trực tiếp SO, AM cùng BN đồng quy.
Hướng dẫn giải:

a) trong mp(ABCD), AB cắt CD tại E.
Ta có: E ∈ AB ⊂ (MAB) ⇒ E ∈ (MAB) ⇒ ME ⊂ (MAB)
E ∈ CD ⊂ (SCD) ⇒ E ∈ (SCD)
Mà M ∈ SC ⊂ (SCD)
⇒ ME ⊂ (SCD).
+ vào mp(SCD), EM cắt SD tại N.
Ta có:N ∈ SD
N ∈ EM ⊂ mp(MAB)
Vậy N = SD ∩ mp(MAB)
b) chứng tỏ SO, MA, BN đồng quy:
+ Trong mặt phẳng (SAC) : SO cùng AM cắt nhau.
+ trong mp(MAB) : MA cùng BN cắt nhau
+ trong mp(SBD) : SO cùng BN cắt nhau.
+ Qua AM cùng BN xác minh được nhất (MAB), nhưng SO không nằm trong mặt phẳng (MAB) nên AM; BN; SO không đồng phẳng.
Vậy SO, MA, BN đồng quy.
Trên đấy là lý thuyết và một vài bài tập toán hình 11 - Đại cưng cửng về đường thẳng và mặt phẳng mà shop chúng tôi đã biên soạn theo chương trình SGK. Hy vọng đây là một tài liệu hữu dụng cho các em. Cảm ơn các em đã theo dõi.









