Kì thi THPTQG là kì thi quan lại trọng hàng đầu đánh dấu bước ngoặt của cuộc đời mỗi học sinh. Trong đó, môn Toán được coi là môn học vô cùng quan trọng tác động đến kết quả tốt nghiệp tương tự như tuyển sinh đại học của những sĩ tử. Nội dung bài viết dưới đây, Cmath sẽ mang về cho chúng ta một cái nhìn tổng quan về chương trình Toán lớp 12. Cùng khám phá nhé!
Chương trình toán lớp 12 bao gồm khó không?
Một thắc mắc được đa số chúng ta học sinh sẵn sàng lên lớp 12 quan liêu tâm. Đó chính là chương trình toán lớp 12 tất cả khó không? Cần làm những gì để học giỏi môn Toán lớp 12? Hy vọng bài viết của công ty chúng tôi sẽ cho bạn cái chú ý khách quan liêu nhất.
Bạn đang xem: Chương trình lớp 12 toán
Chương trình toán lớp 12 tương đối khô khan
Bạn sẽ dễ ợt nhận ra sự phức tạp của môn học tập này nếu chú ý vào chương trình học toán lớp 12. Công tác khá nặng, yêu thương cầu học sinh phải học và hiểu không hề ít nội dung đặc biệt quan trọng như đạo hàm và ứng dụng đạo hàm trong khảo sát và vẽ đồ thị hàm số, nguyên hàm – tích phân với ứng dụng, hàm số lũy thừa, hàm số mũ cùng hàm số Logarit, số phức, khối đa diện, cách thức tọa độ trong ko gian… vì đó, so với lịch trình toán ở các năm học tập trước, môn toán lớp 12 trong khi khô khan rộng hẳn.
Yêu cầu học viên phải nghiêm túc, chuyên chỉ
Toán học luôn yêu cầu học viên phải nên cù, chăm chỉ. Do môn học này có rất nhiều định nghĩa, cách làm mà bắt buộc học sinh phải nỗ lực chắc, hiểu sâu. ở bên cạnh đó, môn toán là môn học luôn có đa dạng và phong phú bài tập. Ở những khối lớp dưới chắc hẳn các em học viên đã thân quen với bài toán làm bài bác tập về nhà môn Toán mỗi ngày. Đặc biệt, môn toán lớp 12 lại con số bài tập cực kỳ nhiều. Bên cạnh việc làm các bài tập vào sách giáo khoa, chúng ta học sinh đề xuất tập làm quen với các bài tập trong những đề thi đại học, đề thi xuất sắc nghiệp của rất nhiều năm trước. Cũng chính vì vậy, môn toán lớp 12 sẽ là một trong thử thách mập nếu như học viên không nghiêm túc, siêng năng học tập.
Chương trình toán lớp 12 mang lại nhiều áp lực
Môn toán lớp 12 sẽ quyết định đến kết quả tốt nghiệp trung học phổ thông và xét tuyển vào những trường đại học của những bạn. Trong năm học trước, các chúng ta có thể lơ là, không tập trung học toán. Nhưng lại ở lớp 12, chúng ta bắt buộc phải học tập với trọng tâm lý rất là nghiêm túc. Chính vấn đề đó sẽ khiến các bạn học sinh chịu áp lực khá lớn khác hoàn toàn với tư tưởng nhởn dơ dáy ở trong năm trước.

Chương trình toán học tập lớp 12 tất cả khó không?
Yêu cầu học viên phải có phương pháp học tập đúng đắn
Để học tốt ngẫu nhiên môn học tập nào, các bạn cũng đều yêu cầu tìm ra phương pháp học tập phù hợp, đúng mực và hiệu quả. Ví dụ, bạn có nhu cầu học xuất sắc môn văn, bạn cần cần mẫn đọc nhiều sách, báo, truyện nhằm phát triển tài năng sử dụng ngữ điệu và truyền đạt phát minh bằng ngôn ngữ của mình. Muốn giỏi âm nhạc thì chúng ta phải luyện tập để tăng khả năng cảm âm, luyện thanh, tham gia những câu lạc bộ âm nhạc để làm quen với sân khấu, cùng tự tin trước đám đông. Bạn sẽ không thể áp dụng phương pháp học văn làm cho môn âm nhạc và ngược lại.
Điều này sẽ gây nên phản tác dụng, bạn nỗ lực cố gắng để học xuất sắc nhưng không hề nhìn thấy được một chút ít tiến bộ, tự đó rất có thể sinh ra ngán nản, mất phương hướng. Đối với công tác toán lớp 12 cũng vậy. Bạn cần phải tìm cho mình một phương thức học tập đúng đắn tương xứng với bạn dạng thân. Giả dụ không, bạn chắc chắn rằng sẽ gặp gỡ rắc rối trong việc tiếp thu, ghi nhớ và vận dụng trọng lượng lớn kỹ năng và kiến thức môn toán lớp 12.
Chương trình toán lớp 12 liên quan đến nhiều kỹ năng lớp dưới
Có thể nói, lịch trình học của các năm đều contact mật thiết cùng với nhau. Loài kiến thức các bạn học sinh sống lớp dưới sẽ là nền tảng tiếp đến phát triển rộng ở chương trình lớp trên. Chính vì vậy, lịch trình toán lớp 12 là tổng hợp các kiến thức các bạn đã được học trong suốt 12 năm học tập qua. Điều này còn có nghĩa rằng, nếu chúng ta không triệu tập học ở trong những năm trước, sẽ chạm chán trở ngại cùng phải nỗ lực nhiều không chỉ có thế khi học tập toán lớp 12.
Yêu cầu học sinh phải sắp đến xếp thời gian hợp lý
Như sẽ biết, những môn học trong lịch trình lớp 12 tất cả vị trí cực kỳ quan trọng vào kỳ thi tốt nghiệp trung học phổ quát và con đường sinh cao đẳng, đại học. Các bạn không chỉ phải tập trung học mỗi môn toán, nhưng còn yêu cầu học tất cả các môn trong khối thi đh và các môn xuất sắc nghiệp. Điều đó có nghĩa là các bạn phải học sao cho vừa bảo vệ điểm số và kỹ năng và kiến thức cho những môn học khác, vừa phải chuyên sâu vào lịch trình toán lớp 12. Vì vậy, vấn đề phân chia thời hạn học tập phải chăng là điều rất là quan trọng trong thời điểm học sau cùng của đời học tập sinh.
Các chương đặc biệt cần chú ý trong toán lớp 12
Căn cứ vào đề minh họa THPT tổ quốc được bộ GD&ĐT ra mắt các năm, các bạn học sinh cần xem xét đặt trung tâm ôn tập vào toàn thể kiến thức khối 12. Ở lịch trình 10, 11, những em chỉ việc ôn tập ở tại mức cơ bản. Những chương đặc biệt chiếm những điểm trong chương trình toán 12 rất có thể kể mang đến như các kiến thức liên quan đến hàm số, hàm số lũy thừa, hàm số mũ với hàm số Logarit, nguyên hàm, tích phân và ứng dụng của tích phân, số phức, khối đa diện…

Các chương đặc trưng cần chú ý trong toán lớp 12
Chương trình học toán lớp 12
Cũng như chương trình toán ở các lớp dưới, lịch trình toán lớp 12 cũng được phân thành hai phần là đại số với hình học. Rứa thể, con kiến thức những chương như sau:
Phần đại số
Đại số cùng giải tích 12 bao gồm 4 chương thiết yếu như sau: vận dụng đạo hàm để khảo sát và vẽ đồ thị hàm của hàm số; hàm số lũy thừa, hàm số mũ cùng hàm số Logarit; nguyên hàm, tích phân và ứng dụng; số phức.
Chương 1: Ứng dụng đạo hàm để khảo sát điều tra và vẽ vật dụng thị của hàm sốỞ chương này, học sinh sẽ vận dụng kiến thức đạo hàm để khảo sát và vẽ đồ vật thị của hàm số. Đồng thời, điều tra khảo sát sự đồng biến, nghịch trở nên của hàm số cùng tìm rất trị của hàm số trên tập xác định của nó.
Bên cạnh đó, những em được luyện tập các dạng toán về tìm giá bán trị bự nhất, giá bán trị nhỏ dại nhất của hàm số. Ko kể ra, học viên được học tập thêm một kiến thức và kỹ năng mới đó là kiến thức và kỹ năng về đường tiệm cận với học cách khảo sát điều tra sự phát triển thành thiên với vẽ đồ gia dụng thị của hàm số.
Chương 2: Hàm số lũy thừa, hàm số mũ cùng hàm số LogaritỞ văn bản này, học sinh sẽ học về hàm số lũy thừa. Đây là một kiến thức mới, cung cấp cho học sinh những loài kiến thức lý thuyết về khái niệm, tính chất, tập xác định, đạo hàm của hàm số lũy thừa,…
Chương này đòi hỏi các bạn học sinh cần nắm cứng cáp những kỹ năng và kiến thức này để rất có thể vận dụng làm các bài tập. Hàm số mũ với hàm số logarit cũng tương tự, phần lớn là những kiến thức và kỹ năng mới đối với học sinh.
Trong đề thi THPT quốc gia luôn mở ra những câu hỏi liên quan mang đến đồ thị. Những thắc mắc này gồm đủ các mức độ từ đơn giản đến phức tạp. Đòi hỏi học viên phải luyện tập rất nhiều ở những bài xích tập dạng này.
Chương 3: Nguyên hàm, tích phân và ứng dụng của tích phânĐây là 1 trong nội dung trọn vẹn mới đối với môn Giải tích lớp 12. Ở chương này, học sinh sẽ được thiết kế quen cùng với các phương thức tìm nguyên hàm, tính tích phân và ứng dụng vào tính thể tích của những vật thể và diện tích hình phẳng.
Nội dung này đựng được nhiều kiến thức kim chỉ nan quan trọng, đòi hỏi học sinh buộc phải ghi nhớ những công thức từ bỏ cơ bản đến nâng cao, mở rộng. Chúng ta cần vắt chắc kim chỉ nan từ đó mới có thể giải được những bài xích tập dạng bài bác này.
Phần nội dung này chứa tương đối nhiều câu vô cùng khó, giúp học viên đạt điểm 9, điểm 10. Cũng chính vì thế, chúng ta cần luyện tập thành thạo các câu dễ dàng và đơn giản trước, sau đó dần dần tăng độ khó, thử thách ở đông đảo câu nâng cao.
Chương 4: Số phứcỞ chương học, các bạn sẽ được làm quen với có mang số phức, những phép toán cộng trừ nhân chia số phức cùng phương trình bậc hai về số phức. Dạng bài bác tập tương quan đến số phức trong đề thi THPTQG khá 1-1 giản. Các bạn chỉ cần nắm rõ những kiến thức triết lý cơ phiên bản là đã có thể dễ dàng tìm điểm ở trong phần này.

Phần đại số
Phần hình học
Phân môn này được chia thành 3 chương: khối đa diện, khía cạnh nón, phương diện trụ, mặt cầu và phương pháp tọa độ trong không gian. Chú ý chung, chương trình hình học lớp 12 triệu tập về các hình học tập không gian. Điều này yên cầu học sinh cần phải có sự cửa hàng hình học mới rất có thể dễ dàng giải được.
Hình học tập 12 được xem như là nội dung hơi khó. Mặc dù nhiên, khi học sinh nắm được cách thức và có sự ảnh hưởng thì rất có thể giải quyết các bài toán một biện pháp dễ dàng.
Bước đầu có tác dụng quen cùng với hình học tập không gian, có thể các bạn sẽ cảm thấy cạnh tranh hiểu cùng nản lòng. Đừng lo khi đã có tác dụng quen một vài dạng bài, các em sẽ cảm xúc sự thú vui của môn học này.

Phần hình học
Tạm kết
Bài viết trên phía trên giúp chúng ta có một cái nhìn tổng quan tiền về chương trình Toán lớp 12. Từ đó giúp các bạn xác định được phương hướng cũng tương tự xây dựng cách thức học tập hòa hợp lý, hiệu quả. Chúc chúng ta học xuất sắc môn toán 12 cùng đạt thành tựu cao vào kỳ thi THPTQG.
Toán 12 là phần đặc biệt quan trọng nhất vào kì thi trung học phổ thông quốc gia, nó chiếm đa phần lượng thắc mắc trong một đề thi. Vày vậy con kiến guru muốn chia sẻ cho các bạn tổng hợp kỹ năng toán lớp 12 chương 1 , liên quan đến vận dụng đạo hàm để khảo sát điều tra hàm số. Nội dung bài viết tổng hợp kim chỉ nan toán 12 cơ bản, ngoài ra còn gửi ra các hướng tiếp cận giải các dạng toán không giống nhau, vậy cho nên các bạn có thể coi như thể tài liệu ôn tập để sẵn sàng cho kì thi chuẩn bị tới. Mời các bạn cùng hiểu và tham khảo nhé:
I. Tổng hợp kiến thức và kỹ năng toán 12: sự đồng vươn lên là và nghịch trở nên của hàm số
1. Lập bảng xét vết của một biểu thức P(x)
Bước 1.Tìm nghiệm của biểu thức P(x), hoặc quý giá của x có tác dụng biểu thức P(x) ko xác định.
Bước 2.Sắp xếp các giá trị của x kiếm được theo vật dụng tự từ bé dại đến lớn.
Bước 3. Sử dụng laptop tìm dấu của P(x) bên trên từng khoảng tầm của bảng xét dấu.
2. Xét tính đơn điệu của hàm số y = f(x) bên trên tập xác định
Bước 1.Tìm tập xác minh D.
Bước 2.Tính đạo hàm y" = f"(x).
Bước 3.Tìm nghiệm của f"(x) hoặc các giá trị x khiến cho f"(x) không xác định.
Bước 4.Lập bảng phát triển thành thiên.
Bước 5. Kết luận.
3. Tìm điều kiện của tham số m nhằm hàm số y = f(x) đồng biến, nghịch biến trên khoảng tầm (a;b) đến trước
mang lại hàm số y = f(x, m) bao gồm tập khẳng định D, khoảng chừng (a; b) ⊂ D:
- Hàm số nghịch phát triển thành trên (a; b) ⇔ y" ≤ 0, ∀ x ∈ (a; b)
- Hàm số đồng trở thành trên (a; b) ⇔ y" ≥ 0, ∀ x ∈ (a; b)
* Chú ý: riêng rẽ hàm số

- Hàm số nghịch biến chuyển trên (a; b) ⇔ y"
- Hàm số đồng biến trên (a; b) ⇔ y" > 0, ∀ x ∈ (a; b)
4. Kĩ năng giải nhanh các bài toán rất trị hàm số bậc bố y = ax3 + bx2 + cx + d (a ≠ 0)
Ta tất cả y" = 3ax2 + 2b x + c
- Đồ thị hàm số bao gồm hai điểm cực trị khi phương trình y" = 0 tất cả hai nghiệm phân biệt
⇔ b2 - 3ac > 0. Khi đó đường trực tiếp qua hai điểm cực trị chính là :
Bấm máy tính tìm đi ra ngoài đường thẳng trải qua hai điểm cực trị :

Hoặc sử dụng công thức:

- khoảng cách giữa nhì điểm rất trị của thứ thị hàm số bậc bố là:

5. Khuyên bảo giải nhanh việc cực trị hàm trùng phương
Cho hàm số: y = ax4 + bx2 + c (a ≠ 0) có đồ thị là (C).

(C) có tía điểm cực trị y" = 0 tất cả 3 nghiệm phân biệt

Khi đó tía điểm rất trị là:

với Δ = b2 - 4ac
Độ dài những đoạn thẳng:

II. Tổng hợp kỹ năng toán lớp 12: giá trị lớn nhất , giá bán trị nhỏ nhất của hàm số
1. Quá trình tìm giá chỉ trị mập nhất, giá chỉ trị bé dại nhất của hàm số sử dụng bảng trở nên thiên
Bước 1.Tính đạo hàm f"(x).
Bước 2.Tìm những nghiệm của f"(x) và các điểm f"(x) trên K.
Bước 3.Lập bảng trở thành thiên của f(x) trên K.
bước 4. địa thế căn cứ vào bảng trở thành thiên tóm lại

2. Quá trình tìm giá trị phệ nhất, giá bán trị bé dại nhất của hàm số không thực hiện bảng biến đổi thiên
a) Trường hòa hợp 1: Tập K là đoạn
-Bước 1.Tính đạo hàm f"(x) .
-Bước 2. Tìm tất cả các nghiệm xi ∈
-Bước 3. Tính f(a), f(b), f( xi ), f( αi ).
-Bước 4. So sánh các giá trị tính được với kết luận

b) Trường thích hợp 2: Tập K là khoảng chừng (a; b)
-Bước 1.Tính đạo hàm f"(x) .
-Bước 2. Tìm tất cả các nghiệm xi ∈ (a; b) của phương trình f"(x) = 0 và tất cả các điểm αi ∈ (a; b) tạo nên f"(x) không xác định.
-Bước 3. Tính

-Bước 4. So sánh những giá trị tính được với kết luận

* Chú ý:Nếu giá trị lớn số 1 (nhỏ nhất) là A hoặc B thì ta kết luận không có giá trị lớn nhất (nhỏ nhất).
III. Tổng hợp lý thuyết toán 12: Đường tiệm cận
1. Quy tắc tìm giới hạn vô cực
Quy tắc kiếm tìm GH của tích f(x).g(x)
Nếu


thì

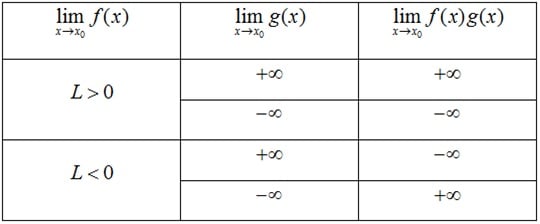
2. Luật lệ tìm số lượng giới hạn của yêu thương 


(Dấu của g(x) xét bên trên một khoảng chừng K nào đó sẽ tính giới hạn, cùng với x ≠ x0 )
Chú ý : những quy tắc trên vẫn đúng cho các trường hợp:

IV. Tổng hợp kỹ năng và kiến thức toán 12: điều tra khảo sát sự biến hóa thiên với vẽ vật dụng thị hàm số
1. Các bước giải bài bác toán khảo sát điều tra và vẽ đồ thị hàm số
- bước 1.Tìm toàn bộ các tập xác minh của hàm số vẫn cho
- cách 2.Tính đạo hàm y" = f"(x) ;
- bước 3.Tìm nghiệm của phương trình ;
- cách 4. Tính giới hạn

- cách 5.Lập bảng biến thiên;
- bước 6.Kết luận tính biến đổi thiên và cực trị (nếu có);
- cách 7.Tìm các điểm quan trọng của thứ thị (giao với trục Ox, Oy, những điểm đối xứng, ...);
- cách 8. Vẽ đồ gia dụng thị.
2. Những dạng đồ vật thị của hàm số bậc 3 y = ax3+ bx2 + cx + d (a ≠ 0)

-Lưu ý:Đồ thị hàm số có 2 điểm rất trị ở 2 phía so với trục Oy khi ac
 3. Các dạng đồ dùng thị của hàm số bậc 4 trùng phương y = ax4 + bx2 + c (a ≠ 0)
3. Các dạng đồ dùng thị của hàm số bậc 4 trùng phương y = ax4 + bx2 + c (a ≠ 0)


4. Những dạng đồ gia dụng thị của hàm số độc nhất biến (ab - bc ≠ 0)
(ab - bc ≠ 0)


5. Biến hóa đồ thị
cho 1 hàm số y = f(x) gồm đồ thị (C) . Lúc đó, với số a > 0 ta có:
- Hàm số y = f(x) + a tất cả đồ thị (C") là tịnh tiến (C) theo phương của Oy lên phía trên a đối kháng vị.
- Hàm số y = f(x) - a tất cả đồ thị (C") là tịnh tiến (C) theo phương của Oy xuống bên dưới a đối chọi vị.
- Hàm số y = f(x + a) tất cả đồ thị (C") là tịnh tiến (C) theo phương của Ox qua trái a solo vị.
- Hàm số y = f(x - a) gồm đồ thị (C") là tịnh tiến (C) theo phương của Ox qua đề xuất a solo vị.
- Hàm số y = -f(x) gồm đồ thị (C") là đối xứng của (C) qua trục Ox.
- Hàm số y = f(-x) bao gồm đồ thị (C") là đối xứng của (C) qua trục Oy.
- Hàm số

+ không thay đổi phần đồ gia dụng thị (C) nằm bên cạnh phải trục Oy và bỏ phần (C) nằm cạnh sát trái Oy.
+ mang đối xứng phần vật dụng thị (C) nằm sát phải trục Oy qua Oy.

- Hàm số có đồ thị (C") bằng cách:
+ không thay đổi phần trang bị thị (C) nằm trên Ox.
+ mang đối xứng phần đồ vật thị (C) nằm bên dưới Ox qua Ox và cho phần đồ thị (C) nằm bên dưới Ox.
Trên đây là tổng hợp kỹ năng và kiến thức toán lớp 12 chương một phần hàm số mà Kiến muốn share đến những bạn, hy vọng thông qua bài viết ở trên, bạn có thể tổng hợp lại những kiến thức và đắp vào phần đông lỗ hổng còn thiếu sót của phiên bản thân. Chương này là 1 trong những chương quan trọng đặc biệt trong kì thi thpt quốc gia, vày vậy các bạn nhớ ôn tập thật kỹ để tự tin khi làm bài bác nhé. Ngoài ra các chúng ta cũng có thể tham khảo các nội dung bài viết khác bên trên trang của loài kiến để có rất nhiều kiến thức có lợi hơn.









