
Giải SGK Toán 10 bài xích 16 (Kết nối tri thức): Hàm số bậc nhị
8.8 K
Tailieumoi.vn ra mắt Giải bài bác tập Toán lớp 10 bài bác 16: Hàm số bậc hai chi tiết sách Toán 10 Tập 2 Kết nối tri thức với cuộc sống giúp học viên xem cùng so sánh lời giải từ đó biết phương pháp làm bài bác tập môn Toán 10. Mời các bạn đón xem:
Giải bài xích tập Toán lớp 10 bài xích 16: Hàm số bậc hai
A. Các thắc mắc trong bài
Mở đầu trang 11Toán 10 Tập 2:Bác Việt tất cả một tấm lưới hình chữ nhật dài trăng tròn m. Bác hy vọng dùng tấm lưới này rào chắn ba mặt áp bên bức tường của căn vườn nhà bản thân thành một mảnh đất nền hình chữ nhật nhằm trồng rau.
Bạn đang xem: Toán lớp 10 bài 16
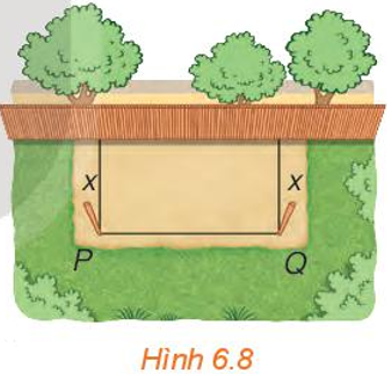
Hỏi nhị cột góc sản phẩm rào rất cần phải cắm cách bức tường bao xa để mảnh đất được rào chắn của chưng có diện tích s lớn nhất?
Lời giải:
Sau bài học này, ta xử lý được việc trên như sau:
Gọi x (mét, x > 0) là khoảng cách từ điểm cọc p và Q mang đến bờ tường.
Tấm lưới dài trăng tròn m và được rào chắn ba mặt như Hình 6.8, đề xuất x + x + PQ = 20.
Do đó, PQ = đôi mươi – x – x = 20 – 2x (m).
Vì PQ > 0 nên trăng tròn – 2x > 0&h
Arr;2x Hoạt rượu cồn 1 trang 11Toán 10 Tập 2:Xét bài toán rào vườn ở trường hợp mở đầu. Gọi x mét (0
a) Độ nhiều năm cạnh PQ của mảnh đất.
b) diện tích s S(x) của mảnh đất nền được rào chắn.
Lời giải:
a) Tấm lưới có chiều dài đôi mươi m, khoảng cách từ điểm gặm cọc tới bức tường là x (m), đóng 2 cọc p và Q, mỗi cọc phương pháp tường x (m).
Tấm lưới rào chắn 3 mặt như Hình 6.8 bắt buộc x + x + PQ = 20.
Vậy độ nhiều năm cạnh PQ của mảnh đất nền là: đôi mươi – x – x = trăng tròn – 2x (m).
b) mảnh đất được rào chắn là 1 trong những hình chữ nhật có hai size là x (m) và đôi mươi – 2x (m).
Diện tích S(x) của mảnh đất nền được rào chắn là: S(x) = x . (20 – 2x) = – 2x2+ 20x.
Câu hỏi trang 12Toán 10 Tập 2:Hàm số như thế nào dưới đây là hàm số bậc hai?
A. Y = x4 + 3x2 + 2.
B.y=1x2.
C. Y = – 3x2+ 1.
D.y=31x2+31x−1.
Lời giải:
Đáp án đúng là: C
Hàm số bậc nhị là hàm số cho bởi phương pháp y = ax2+ bx + x với a, b, c là các hằng số và a ≠ 0.
Vậy trong số hàm số đã cho thì hàm số C. Y = – 3x2+ một là hàm số bậc hai với những hệ số a = – 3, b = 0 và c = 1.
Hàm số ở lời giải A chưa phải là hàm số bậc nhì vì có bậc của x là 4.
Hàm số ở đáp án B chưa phải là hàm số bậc hai vì chứa ẩn ở bên dưới mẫu nên nó là phân thức.
Hàm số ở giải đáp D không phải là hàm số bậc hai do chứa ẩn ở dưới mẫu, nếu ta đặt1x=tthì lúc ấy ta sẽ có được được hàm số bậc nhị theo t.
Luyện tập 1 trang 12Toán 10 Tập 2:Cho hàm số y = (x – 1)(2 – 3x).
a) Hàm số sẽ cho có phải là hàm số bậc hai không? trường hợp có, hãy khẳng định các hệ số a, b, c của nó.
b) ráng dấu “?” bằng những số phù hợp để hoàn thành bảng báo giá trị sau của hàm số đang cho.
x | – 2 | – 1 | 0 | 1 |
y | ? | ? | ? | ? |
Lời giải:
a) Ta có: (x – 1)(2 – 3x) = 2x – 3x2– 2 + 3x = – 3x2+ 5x – 2.
Hay y = = – 3x2+ 5x – 2.
Đây là hàm số bậc nhị với những hệ số a = – 3, b = 5, c = – 2.
Vậy hàm số đã chỉ ra rằng hàm số bậc hai.
b) cố kỉnh lần lượt các giá trị của x vào hàm số nhằm tính cực hiếm của y tương ứng.
Với x = – 2 thì y = – 3 . (– 2)2+ 5 . (– 2) – 2 = – 24.
Với x = – 1 thì y = – 3 . (– 1)2+ 5 . (– 1) – 2 = – 10.
Với x = 0 thì y = – 3 . 02+ 5 . 0 – 2 = – 2.
Với x = 1 thì y = – 3 . 12+ 5 . 1 – 2 = 0.
Vậy ta điền vào bảng như sau:
x | – 2 | – 1 | 0 | 1 |
y | – 24 | – 10 | – 2 | 0 |
Vận dụng 1 trang 12Toán 10 Tập 2:Một viên bi rơi tự do thoải mái từ chiều cao 19,6 m xuống mặt đất. Độ cao h (mét) đối với mặt khu đất của viên bi trong khi rơi phụ thuộc vào vào thời gian t (giây) theo công thức: h = 19,6 – 4,9t2; h, t ≥ 0.
a) Hỏi sau từng nào giây kể từ khi rơi thì viên bi chạm đất?
b) tìm tập xác minh và tập quý giá của hàm số h.
Lời giải:
a) Viên bi rơi đụng đất lúc h = 0.
Hay 19,6 – 4,9t2= 0&h
Arr;4,9t2= 19,6&h
Arr;t2= 4&h
Arr;t = 2 hoặc t = – 2.
Vì t ≥ 0 bắt buộc t = 2 thỏa mãn.
Vậy sau 2 giây kể từ lúc rơi thì viên bi chạm đất.
Xem thêm: Đề Thi Toán Lớp 12 Kì 1 Toán Lớp 12 Có Đáp Án Và Lời Giải Chi Tiết
b) h = 19,6 – 4,9t2
Đây là hàm số bậc nhị với trở nên t, mà t ≥ 0.
Do đó, tập xác minh của hàm số h là D = <0; + ∞).
t2≥ 0 với tất cả t
&h
Arr;– 4,9t2≤ 0 với tất cả t
&h
Arr;– 4,9t2+ 19,6 ≤ 0 + 19,6 với tất cả t
&h
Arr;19,6 – 4,9t2≤ 19,6 với đa số t.
Do kia h ≤ 19,6 với đa số t.
Lại bao gồm h ≥ 0 (theo đề bài).
Nên 0 ≤ h ≤ 19,6 với tất cả t.
Vậy tập quý giá của hàm số h là <0; 19,6>.
Hoạt động 2 trang 12Toán 10 Tập 2:Xét hàm số y = S(x) = – 2x2+ 20x (0
a) trên mặt phẳng tọa độ Oxy, trình diễn tọa độ các điểm trong bảng giá trị của hàm số lập được sống Ví dụ 1. Nối các điểm đã vẽ lại ta được dạng đồ thị hàm số y = – 2x2+ 20x trên khoảng chừng (0; 10) như trong Hình 6.10. Dạng đồ gia dụng thị của hàm số y = – 2x2+ 20x tất cả giống với vật dụng thị của hàm só y = – 2x2hay không?
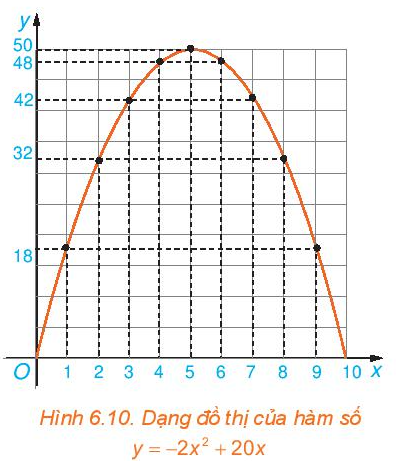
b) Quan cạnh bên dạng thứ thị của hàm số y = – 2x2+ 20x vào Hình 6.10, tìm tọa độ điểm tối đa của đồ thị.
c) triển khai phép biến chuyển đổi
y = – 2x2+ 20x = – 2(x2– 10x) = – 2(x2– 2 . 5 . X + 25) + 50 = – 2(x – 5)2+ 50.
Hãy cho biết giá trị lớn nhất của diện tích mảnh khu đất được rào chắn. Từ kia suy ra giải thuật của bài toán tại phần mở đầu.
Lời giải:
a) Biểu diễn những điểm bao gồm tọa độ (0; 0), (2; 32), (4; 48), (5; 50), (6; 48), (8; 32), (10; 0) lên khía cạnh phẳng tọa độ với nối lại được của thứ thị hàm số y = – 2x2+ 20x trên khoảng chừng (0; 10).
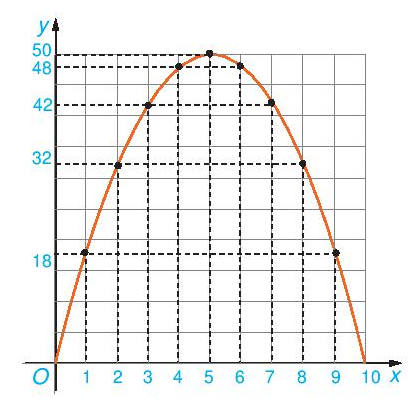
Quan giáp hình ta thấy, dạng của đồ gia dụng thị hàm số y = – 2x2+ 20x tương đương với dạng của đồ thị hàm số y = – 2x2.
b) Tọa độ điểm tối đa của đồ dùng thị hàm số y = – 2x2+ 20x là (5; 50).
c) vì chưng (x – 5)2≥ 0 với mọi số thực x
Nên – 2(x – 5)2≤ 0 với tất cả số thực x
Do đó: – 2(x – 5)2+ 50 ≤ 0 + 50 = 50 với tất cả số thực x.
Vậy y ≤ 50.
Vậy giá trị lớn số 1 của y là 50 hay diện tích lớn tốt nhất của mảnh đất được rào chắn là 50 m2.
Từ đó ta có giải thuật bài toán mở đầu:
Gọi x (mét, x > 0) là khoảng cách từ điểm cọc phường và Q mang đến bờ tường.
Tấm lưới dài 20 m cùng được rào chắn như Hình 6.8 buộc phải x + x + PQ = 20.
Suy ra: PQ = trăng tròn – x – x = 20 – 2x (m).
Vì PQ > 0 nên đôi mươi – 2x > 0&h
Arr;2x Hoạt cồn 3 trang 13Toán 10 Tập 2:Tương từ HĐ2, ta tất cả dạng thứ thị của một trong những hàm số bậc hai sau.
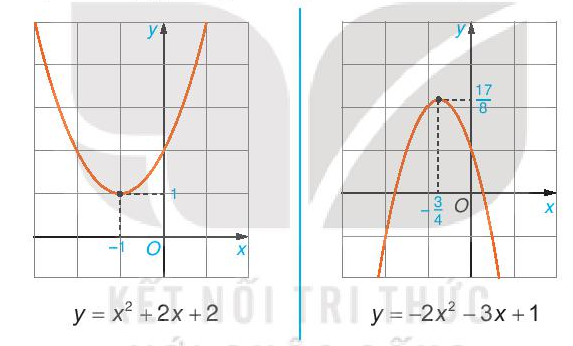
Từ những đồ thị hàm số trên, hãy nêu nội dung cầm cố vào ô gồm dấu “?” trong bảng sau đến thích hợp.
Để học tốt bàiHàm số bậc hai,HỌC247xin mời những em học sinh cùng xem thêm bài giảng bên dưới đây bao gồm các kỹ năng và kiến thức được trình bày cụ thể và đưa ra tiết, thuộc với các dạng bài tập minh họa giúp các em tiện lợi nắm vững vàng được giữa trung tâm bài học.
1. Nắm tắt lý thuyết
1.1. Có mang hàm số
1.2. Đồ thị của hàm số
1.3. Sự đồng biến, nghịch vươn lên là của hàm số
2. Bài bác tập minh họa
3. Luyện tập
3.1. Bài tập trắc nghiệm
3.2. Bài tập SGK
4. Hỏi đáp bài xích 15 Toán 10 KNTT

Nhận xét
Hàm số (y = ax^2(a e 0)) vẫn học sinh hoạt lớp 9 là một trong trường hợp đặc biệt của hàm số bậc nhị với a = c = 0.
Ví dụ: Xét hàm số bậc nhì y = -2x2 + 10x. Thế dấu "?" bằng những số phù hợp để trả thành bảng báo giá trị sau của hàm số.

Giải
Thay các giá trị của x vào công thức hàm số, ta được:

Gọi (P0) là Parabol y = ax2. Ví như ta "dịch chuyển" (P0) theo vectơ(overrightarrow OI ) thì ta đã thu được thiết bị thị (P) của hàm sốy = ax2+ bx + c gồm dạng như hình sau:
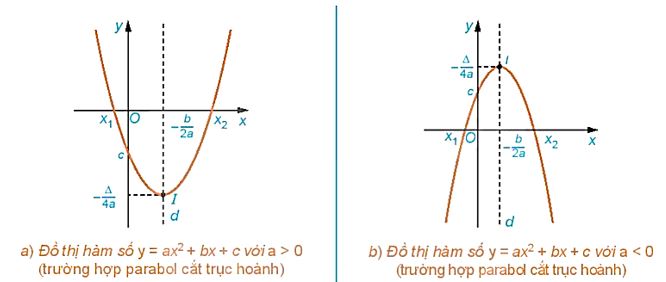
Nhận xét: Đồ thị hàm sốy = ax2+ bx + c(left( a e 0 ight)) là một parabol.
Ví dụ: Vẽ parabol y = -2x2 - 2x + 4.
b) Từ thiết bị thị, hãy tìm khoảng tầm đồng biến, nghịch biến đổi và giá chỉ trị lớn số 1 của hàm số y = -2x2- 2x + 4..
Giải
a) Ta tất cả a = -2 2- 2x + 4, tức là x = 1 cùng x = -2.
Để vẽ vật dụng thị chinh xác hơn, ta rất có thể lấy thêm điểm đối xửng cùng với A qua trục đối xứng(x = - frac12) là(Bleft( - 1;4 ight)).
b) Từ thứ thị ta thầy:
+ Hàm số y = -2x2- 2x + 4 đồng đổi thay trên (left( - infty ; - frac12 ight))nghịch biến hóa trên(left( - frac12; + infty ight));
+ giá bán trị lớn số 1 của hàm số là(y = frac92), lúc (x = - frac12).
Câu 1:Một viên bi rơi thoải mái từ độ dài 19,6 m xuống phương diện đất. Độ cao h (mét) so với mặt đất của viên bi trong những lúc rơi dựa vào vào thời gian t (giấy) theo công thức: h = (19,6-4,9t^2); (h, tgeq 0).
a. Hỏi sau bao nhiêu giây kể từ khi rơi viên bi chạm đất?
b. Tra cứu tập khẳng định và tập quý hiếm của hàm số h.
Hướng dẫn giải
a. Viên bị va đất khi h = 0
Hay (19,6-4,9t^2=0)
(Leftrightarrow 4,9t^2=19,6\Leftrightarrow t^2=4\Rightarrow t=2) (do (tgeq 0).)
Vậy sau 2 giây kể từ lúc rơi viên bi chạm đất.
b. Tập xác định: D = (<0; +infty ))
Ta có: (t^2geq 0Rightarrow 19,6-4,9t^2leq 19,6)
Tập giá trị: (<0;19,6>).
Câu 2:Vẽ parabol (y=3x^2-10x+7). Từ đó tìm khoảng chừng đồng biến, nghịch phát triển thành và giá bán trị bé dại nhất của hàm số (y=3x^2-10x+7).








