Sau khi đã mày mò về định nghĩa Khối đa diện ở bài trước, bài học này vẫn tiếp tục reviews đến các em ráng nào là một đa diện lồi, những bài bác tập đo lường và tính toán trong lịch trình phổ thông số đông được thi công trên một số loại đa diện này. Bên cạnh đó bài học còn trình diễn khái niệm và những loại đa diện đều. Bạn đang xem: Giải toán hình lớp 12 bài 2
1. Video bài giảng
2. Bắt tắt lý thuyết
2.1. Khối nhiều diện lồi
2.2. Khối đa diện đều
3. Bài xích tập minh hoạ
4. Luyện tập bài 2 Hình học tập 12
4.1. Trắc nghiệm
4.2. Bài xích tập SGK
5. Hỏi đáp về tính chất khối đa diệnlồi với khối đa diện đều

- Khối nhiều diện (H) được điện thoại tư vấn là khối đa diện lồi nếu như đoạn thẳng nối nhị điểm bất kì của (H) luôn thuộc (H). Khi ấy đa diện giới hạn (H) được hotline làđa diện lồi.

-Một khối đa diện là khối nhiều diện lồi khi còn chỉ khi miền trong của nó luôn luôn nằm về một phía so với mỗi mặt phẳng đi qua 1 mặt của nó.
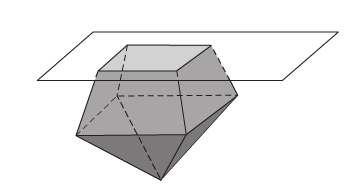
-Một khối đa diện lồi được call làkhối nhiều diện đềuloại p,q nếu:
+Mỗi mặt của nó là 1 đa giác đều p. Cạnh.
+Mỗi đỉnh của chính nó là đỉnh thông thường của đúng q mặt.
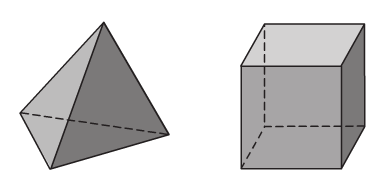
-Các mặt của khối đa diện các là các đa giác gần như và bằng nhau.
-Có năm loại khối đa diện đều. Đó là các khối đa diện đều loại 3,3, loại 4,3,loại 3,4, nhiều loại 5,3, và nhiều loại 3,5.
-Tùy theo số phương diện của chúng, năm nhiều loại khối nhiều diện đầy đủ kể trên theo theo sản phẩm công nghệ tự được điện thoại tư vấn là khối nhiều diện đều, khối lập phương, khối tám khía cạnh đều, khối mười nhì mặt đều, khối nhị mươi mặt đều.


-Hai khối đa diện đều có cùng số khía cạnh và có cạnh đều nhau thì bởi nhau.
-Hai khối đa diện đều phải sở hữu cùng số khía cạnh thì đồng dạng với nhau.
Bài tập minh họa
Bài tập 1:Đếm số đỉnh, số cạnh của khối chén diện đều.
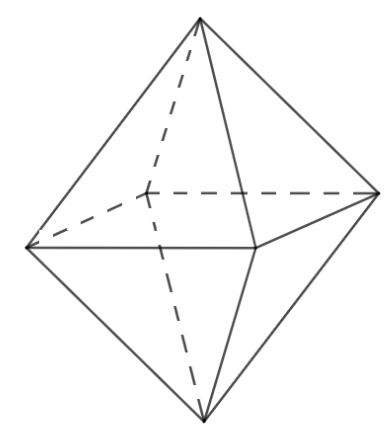
Lời giải
Khối chén bát diện đều sở hữu 6 đỉnh cùng 12 cạnh.
Xem thêm: Giải Toán 10 Toán Cánh Diều ), Toán 10, Giải Toán Lớp 10 Cánh Diều
Bài tập 2:Chứng minh rằng tam giác (IEF, IFM, IMN, INE, JEF, JFM, JMN) cùng (JNE) là đầy đủ tam giác phần đông cạnh bởi ( dfrac a 2)

Lời giải
(ABCD) là tứ diện phần lớn ⇒ tam giác (ABC) đầy đủ (⇒ AB = BC = CA = a)
(I, E, F) thứu tự là trung điểm của những cạnh (AC, AB, BC) yêu cầu ta có (IE, IF, EF) là những đường vừa phải của tam giác (ABC)
(eqalign& Rightarrow IE = 1 over 2BC = 1 over 2a cr& mIF = 1 over 2AB = 1 over 2a cr& mEF = 1 over 2AC = 1 over 2a cr )
Nên tam giác (IEF) là tam giác mọi cạnh bằng(dfrac a 2)
Chứng minh tựa như ta có:(IFM, IMN, INE, JEF, JFM, JMN) với (JNE) là phần đông tam giác phần lớn cạnh bằng(dfrac a 2)
4. Rèn luyện Bài 2 Hình học 12
Sau lúc đã tò mò về khái niệmKhối nhiều diệnở bài xích trước, bài học này đã tiếp tục trình làng đến các em cầm nào làmột đa diện lồi, những bài tập đo lường và tính toán trong công tác phổ thông các được xây dừng trên một số loại đa diện này. Dường như bài học còn trình bày khái niệm và các loạiđa diện đều.
4.1 Trắc nghiệm
Để củng cố bài học kinh nghiệm xin mời các em thuộc làm bài kiểm tra Trắc nghiệm Hình học 12 Chương 1 bài xích 2 để khám nghiệm xem tôi đã nắm được nội dung bài học kinh nghiệm hay chưa.
Câu 1:Trong các mệnh đề sau, mệnh đề như thế nào sai?
A.Hình tạo vì chưng hai tứ diện hầu như ghép cùng với nhau là 1 đa diện lồi.B.Tứ diện là đa diện lồi.C.Hình lập phương là đa diện lồi.D.Hình vỏ hộp là nhiều diện lồi.
Câu 2:
Khối chén bát diện những là khối đa diện đều nhiều loại nào?
A.5;3B.3;5C.4;3D.3;4
Câu 3:
Trong các xác định sau, xác minh nào sai?
A.Chỉ gồm năm mô hình đa diện đều.B.Hình vỏ hộp chữ nhật tất cả diện tích những mặt cân nhau là hình nhiều diện đều.C.Tâm những mặt của hình lập phương chế tạo thành nhiều diện đều.D.Hình chóp tam giác mọi là hình nhiều diện đều.
Câu 4-10:Mời những em singin xem tiếp câu chữ và thi thử Online nhằm củng cố kiến thức và kỹ năng và nắm vững hơn về bài học này nhé!
4.2 bài xích tập SGK
Bên cạnh đó những em có thể xem phần khuyên bảo Giải bài bác tập Hình học 12 Chương 1 bài 2sẽ giúp những em cố kỉnh được các phương pháp giải bài xích tập từ SGKHình học tập 12Cơ phiên bản và Nâng cao.
bài bác tập 1 trang 18 SGK Hình học tập 12
bài tập 2 trang 18 SGK Hình học tập 12
bài bác tập 3 trang 18 SGK Hình học tập 12
bài tập 4 trang 18 SGK Hình học tập 12
bài tập 1.6 trang 12 SBT Hình học 12
bài xích tập 1.7 trang 12 SBT Hình học 12
bài tập 1.8 trang 12 SBT Hình học tập 12
bài bác tập 1.9 trang 12 SBT Hình học 12
bài bác tập 6 trang 15 SGK Hình học tập 12 NC
bài tập 7 trang 15 SGK Hình học 12 NC
bài xích tập 8 trang 15 SGK Hình học 12 NC
bài xích tập 9 trang 15 SGK Hình học tập 12 NC
bài bác tập 10 trang 15 SGK Hình học 12 NC
bài xích tập 11 trang 20 SGK Hình học tập 12 NC
bài tập 12 trang trăng tròn SGK Hình học tập 12 NC
bài bác tập 13 trang trăng tròn SGK Hình học tập 12 NC
bài tập 13 trang 20 SGK Hình học tập 12 NC
bài bác tập 14 trang trăng tròn SGK Hình học tập 12 NC
5. Hỏi đáp vềkhối nhiều diện lồi và khối nhiều diện đều
Nếu có vướng mắc cần giải đáp những em có thể để lại thắc mắc trong phần
Hỏiđáp, xã hội Toán HỌC247 đã sớm vấn đáp cho các em.
-- hack Toán học tập 12 HỌC247

NONE
Bài học thuộc chương
Hình học 12 bài xích 1: định nghĩa về khối đa diện
Hình học 12 bài bác 3: khái niệm về thể tích của khối nhiều diện
Hình học 12 Ôn tập chương 1 Khối đa diện
ADSENSE
ADMICRO
cỗ đề thi nổi bật

UREKA
AANETWORK
13">
XEM nhanh CHƯƠNG TRÌNH LỚP 12
Toán 12
Lý thuyết Toán 12
Giải bài tập SGK Toán 12
Giải BT sách nâng cao Toán 12
Trắc nghiệm Toán 12
Giải tích 12 Chương 4
Đề thi HK2 môn Toán 12
Ngữ văn 12
Lý thuyết Ngữ Văn 12
Soạn văn 12
Soạn văn 12 (ngắn gọn)
Văn mẫu mã 12
Hồn Trương Ba, da hàng thịt
Đề thi HK2 môn Ngữ Văn 12
Tiếng Anh 12
Giải bài Tiếng Anh 12
Giải bài xích Tiếng Anh 12 (Mới)
Trắc nghiệm giờ đồng hồ Anh 12
Unit 16 Lớp 12
Tiếng Anh 12 new Unit 9
Đề thi HK2 môn tiếng Anh 12
Vật lý 12
Lý thuyết đồ Lý 12
Giải bài xích tập SGK đồ dùng Lý 12
Giải BT sách cải thiện Vật Lý 12
Trắc nghiệm thiết bị Lý 12
Vật lý 12 Chương 7
Đề thi HK2 môn thiết bị Lý 12
Hoá học 12
Lý thuyết Hóa 12
Giải bài xích tập SGK Hóa 12
Giải BT sách nâng cao Hóa 12
Trắc nghiệm Hóa 12
Hoá học tập 12 Chương 8
Đề thi HK2 môn Hóa 12
Sinh học 12
Lý thuyết Sinh 12
Giải bài xích tập SGK Sinh 12
Giải BT sách nâng cấp Sinh 12
Trắc nghiệm Sinh 12
Ôn tập Sinh 12 Chương 8 + 9 + 10
Đề thi HK2 môn Sinh 12
Lịch sử 12
Lý thuyết lịch sử hào hùng 12
Giải bài bác tập SGK lịch sử vẻ vang 12
Trắc nghiệm lịch sử hào hùng 12
Lịch Sử 12 Chương 5 lịch sử VN
Đề thi HK2 môn lịch sử hào hùng 12
Địa lý 12
Lý thuyết Địa lý 12
Giải bài xích tập SGK Địa lý 12
Trắc nghiệm Địa lý 12
Địa Lý 12 Địa Lý Địa Phương
Đề thi HK2 môn Địa lý 12
GDCD 12
Lý thuyết GDCD 12
Giải bài bác tập SGK GDCD 12
Trắc nghiệm GDCD 12
GDCD 12 học tập kì 2
Đề thi HK2 môn GDCD 12
Công nghệ 12
Lý thuyết công nghệ 12
Giải bài xích tập SGK công nghệ 12
Trắc nghiệm công nghệ 12
Công nghệ 12 Chương 6
Đề thi HK2 môn technology 12
Tin học 12
Lý thuyết Tin học 12
Giải bài bác tập SGK Tin học 12
Trắc nghiệm Tin học 12
Tin học 12 Chương 4
Đề thi HK2 môn Tin học 12
Cộng đồng
Hỏi đáp lớp 12
Tư liệu lớp 12
Xem những nhất tuần
Đáp án đề thi thpt QG năm 2023
Video: bà xã nhặt của Kim Lân
Đề cương cứng HK2 lớp 12
Video ôn thi thpt QG môn Hóa
Video ôn thi trung học phổ thông QG môn Toán
Video ôn thi trung học phổ thông QG môn Sinh
Video ôn thi thpt QG môn Văn
Video ôn thi thpt QG môn vật lý
Video ôn thi trung học phổ thông QG giờ Anh
Tuyên Ngôn Độc Lập
Khái quát lác văn học việt nam từ đầu CMT8 1945 đến cầm cố kỉ XX
Vợ Nhặt
Đất Nước- Nguyễn Khoa Điềm
Chiếc thuyền không tính xa
Tây Tiến
Rừng xà nu
Vợ ck A Phủ
Việt Bắc
Những người con trong gia đình
Kết nối với chúng tôi
TẢI ỨNG DỤNG HỌC247


Thứ 2 - máy 7: tự 08h30 - 21h00
hoc247.vnThỏa thuận sử dụng
Đơn vị chủ quản: công ty Cổ Phần giáo dục HỌC 247
Chịu trọng trách nội dung: Nguyễn Công Hà - Giám đốc công ty CP giáo dục và đào tạo Học 247
Cho hình lập phương (H). điện thoại tư vấn (H’) là hình chén diện đều phải sở hữu các đỉnh là tâm những mặt của (H). Tính tỉ số diện tích toàn phần của (H) và (H’).
Đề bài
Cho hình lập phương ((H)). Call ((H’)) là hình chén diện đều phải sở hữu các đỉnh là tâm các mặt của ((H)). Tính tỉ số diện tích toàn phần của ((H)) với ((H’)).
Phương pháp giải - Xem đưa ra tiết

+) bát diện đông đảo là khối đa diện bao gồm 8 khía cạnh là 8 tam giác đều.
+) diện tích toàn phần của hình chén diện các = 8. Diện tích s 1 mặt.

Giả sử khối lập phương tất cả cạnh bằng (a). Khi đó diện tích toàn phần của nó là: (S_1 = 6a^2)
Gọi (M) là trung khu của hình vuông vắn (ABCD); (Q) là tâm hình vuông (ADD"A"); (P) là tâm hình vuông vắn (ABB"A"); (N) là tâm hình vuông (BCC"B"); (E) là tâm hình vuông (DCC"D") cùng (F) là tâm hình vuông vắn (A"B"C"D").
Xét chén diện số đông thu được, khi đó diện tích s toàn phần của nó là (8) lần diện tích tam giác số đông (MQE) (hình vẽ)
Xét tam giác (ACD’), ta tất cả (M, Q) lần lượt là trung điểm của (AC) và (AD’) đề nghị (MQ) là đường trung bình của tam giác (ACD’), do đó (MQ = displaystyle1 over 2C mD" = displaystyleasqrt 2 over 2 )
Ta bao gồm (S_MQE = displaystyle1 over 2left( displaystyleasqrt 2 over 2 ight)^2.sqrt 3 over 2 = sqrt 3 a^2 over 8 )
Diện tích bao bọc của bát diện phần lớn là: (S_2 = 8.displaystylesqrt 3 a^2 over 8 = a^2sqrt 3 )
Do đó: (displaystyleS_1 over S_2 = 6 ma^2 over a^2sqrt 3 = 2sqrt 3 )








